Assignment 4: The Incenter of a Triangle

By Kendyl Wade

 

 

The incenter of a triangle is the point inside a triangle that is equidistant from all three sides.

This point also lies on the angle bisectors of the triangle, so we can construct the point by first constructing the bisectors.

Note: This triangle ABC is not a right triangle.

 

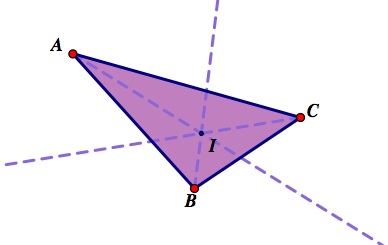
The incenter is the center of the circle inscribed in the triangle, or the incircle.

An excenter is the center of an excircle of a triangle. There are three excircles and excenters.

Here, the excenters are light blue and the excircles are the thin-line, green circles.

 

 

Notice that the excenters create a larger triangle with the original triangle ABC inscribed in it.

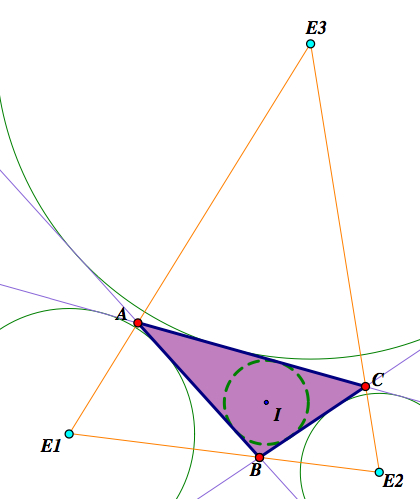
The sides of this larger triangle are actually the bisectors of the exterior angles of the triangle ABC.

If we look as this construction with all the exterior and interior angles showing, we can make some discoveries.

Here we see that every interior angle bisector is concurrent with the two opposite exterior angle bisectors.

Why is that?

Well, first we can say because an angle bisector is always perpendicular to its exterior angle bisector. Then goes through point E3, so since is perpendicular to one side of the triangle and also goes through the point of the opposite vertex, must be an altitude of . Now we can notice that the rays that started out as the angle bisectors of our original triangle are now the altitudes of the triangle made by the excenters. This also means that the incenter, point I, of is also the circumcenter of .

Return