

Final Assignment: Trisecting a Segment
By Kendyl Wade
Trisecting a Segment: Part 1
Step A: Construct a segment AB.
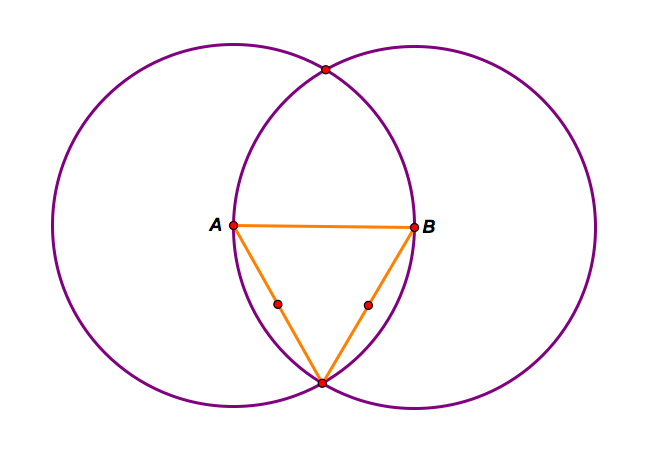
Step B: Construct a circle with center A and radius AB and a circle with center B and radius AB. Then construct segments with A and B and one of the intersections of the two circles. Also, mark the midpoints of those two chords.
Step C: Construct segments connecting the midpoints to the opposite intersection of the circles.
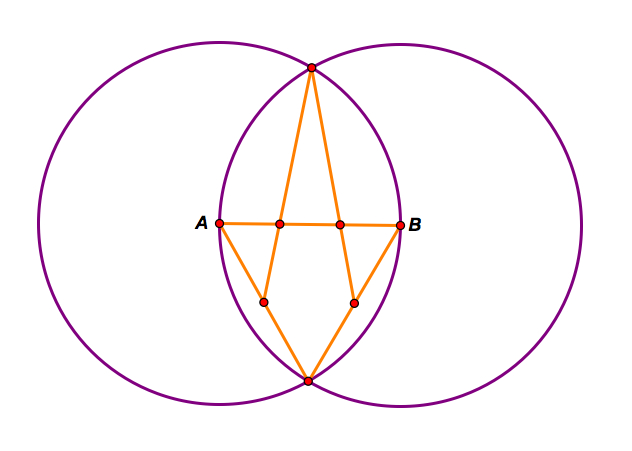
This trisects the segment. Notice the triangle created from the intersections of the circles and the point A. The segment from the top intersection to the midpoint is a median. Thus the intersection would be a centroid and create a ratio of 1:3, therefore doing the same thing to the other half of AB would result in the trisection of AB.
Trisecting a Segment: Part 2
Step A: Construct a segment AB and a ray AC.
Step B: Construct a circle with center C and radius AC. Continue constructing circles with radius AC down the ray until you have three circles.
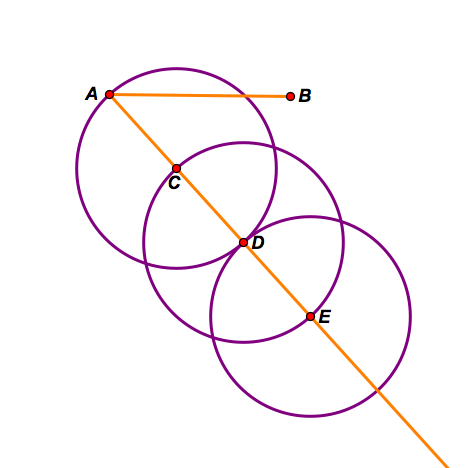
Step C: Construct the segment BE. Then construct two lines parallel to segment BE: one that goes through point D and one that goes through point C.
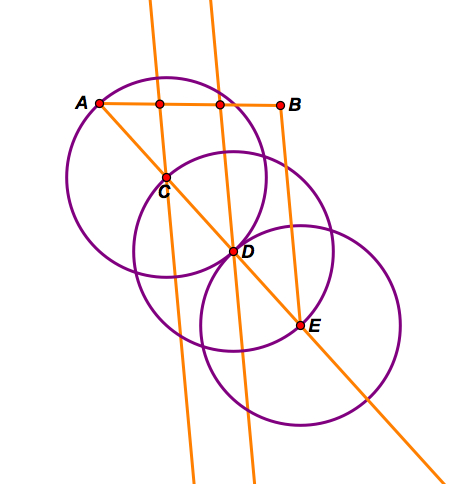
The intersections of these parallel lines and segment AB will be the trisection of segment AB. You could in fact cut a segment up into however many equal pieces you wanted with this method. If you wanted your segment to be in x equal pieces, you would construct x circles down the ray and construct a segment between B and the center of the final circle. Then create lines parallel to that last segment that go through each circle's center. This works because of the Intercept theorem.
Trisecting a Segment: Part 3
This construction is similar to Part 2. Both constructions use common ratios to trisect the segment.
Step A: Construct a segment AB and a ray AC.
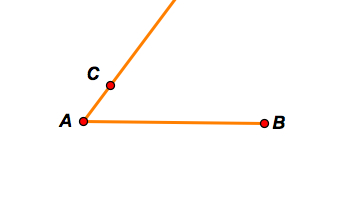
Step B: Construct a circle with center A and radius AC.
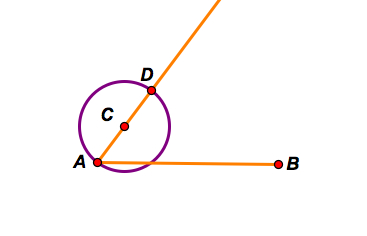
Step C: Construct a line that is parallel to ray AC and goes through the point B. Then construct a circle with center B and radius AC. Then construct another circle with center E and radius AC.
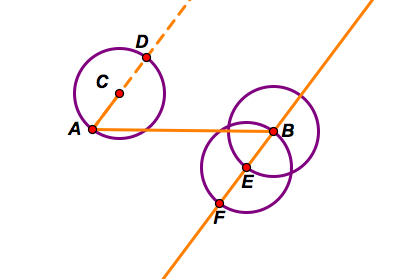
Step D: Next construct segments CF and DE. The intersection of these segments will trisect segment AB.
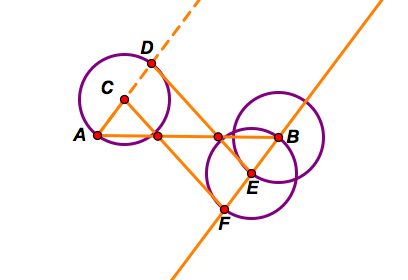
This method also uses the Intercept theorem with a ratio of 1:3.
Trisecting a Segment: Part 4
Step A: Construct a segment AB and a line BC.
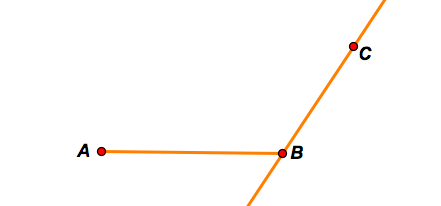
Step B: Construct a circle with center B and radius length BC. Then mark the intersection of line BC and the circle and label the point D.
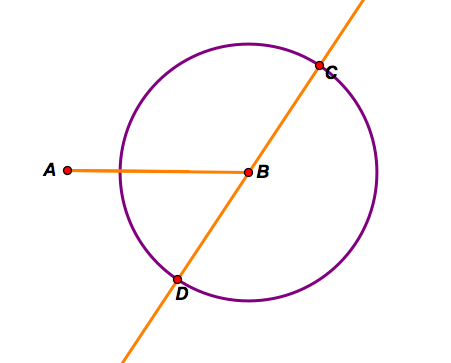
Step C: Next, construct the segment AD and mark the midpoint E.
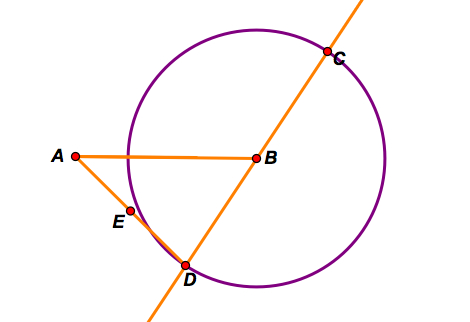
Step D: Finally, construct a segment EC and mark the intersection of segment EC and segment AB as the point F.
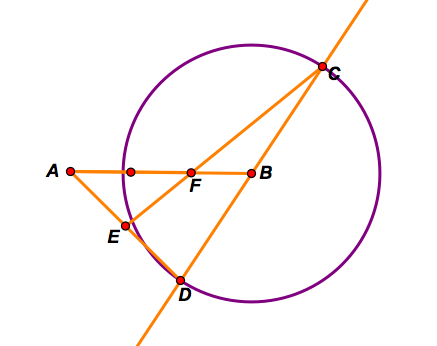
For triangle ACD, point F would be the centroid. By definition of the centroid, segment FB is 1/3 of segment AB.