

Objective: We will explore the sine function and the various transformations that can accompany it. We will then use what we have learned about the transformations to predict what several sine functions will look like.
Review
This exploration is intended for students who are familiar with the sine function. As a review we will first briefly look at the graph and talk about some function properties.
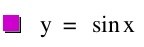
The sine function is one of our basic trigonometric functions. We can describe the sine function as periodic and odd. It has a period of 2π. Thus sin(m)=sin(m+2kπ) where k is any integer. Because sine is odd, then sin(-m)=-sin(m). Using these properties can help students predict the output for a variety of sine functions apart from the basic y=sin(x).
Changing Parameters
Our goal is to explain the parameters a, b, and c in the following sine function.
To gauge changes in our transformations, we will first set a,b, and c equal to 1. The graph is below.
Changing Parameters: a
We will first explore the parameter of a and then mathematically interpret these changes.
When you multiply the sine function by a scalar, what changes do you expect the graph to display? Let's check!
When we look at a couple of examples it appears that the sine function is being stretched vertically. Note that the scalars of a have all been whole numbers. Lets look at what happens when a is less than 1.
When we look at a couple of examples it appears that the sine function is being shrunk vertically.
What we have explored is that by changing the parameter a we have changed the amplitude. Now we will look at various values of a from -5 to 5.
Do we expect the negative scalars to act just like the positive scalars did?
Changing Parameters: b
Next will first explore the parameter of b and then mathematically interpret these changes.
When you multiply the variable x by a scalar b, what changes do you expect the graph to display? Let's check!
When we look at a couple of examples it appears that the sine function is being stretched horizontally. The period in these sine functions is no longer 2π. The period for the function in purple and teal is less than 2π. Note that the values of b have all been greater than one. Lets look at what happens when b is less than 1.
The period for the function in purple and teal is now greater than 2π. What we have explored is how changing the parameter b changes the period of the function. Now we will look at various values of b from -5 to 5.
Do we expect the negative scalars to act just like the positive scalars did?
Changing Parameters: c
Lastly will first explore the parameter of c and then mathematically interpret these changes.
When you change the scalar c, what do you expect the graph to display? Let's check!
When we look at a couple of examples it appears that the sine function is shifting horizontally. We call this transformation a phase shift. The shape of the sine function is preserved, but the location is altered. Now we will look at various values of c from -5 to 5.
Do we expect the negative scalars to act just like the positive scalars did?
Predict
We are now in the position to predict how a sine function behaves before looking at the graph. Let us predict the following function.
First we explore how the scalar multiple of 2 changes the function. This value of a is positive and greater than 2. Thus I know the amplitude will increase and will stretch the the function vertically. The peak of the sine waves will be 2 and -2. Next we explore the b value of 1/3. Note this is positive and less than 1. The period of the sine function will be greater than 2π. Last we explore the c value of -4. Note the absolute value of this c value is greater than one and is negative. This phase shift will be to the right. Let us check our prediction.