Graphs in the xb Plane

Lindsey Harrison

Objective: In this exploration we will examine quadratics in the xb plane. Instead of finding roots through algebraic procedures, the goal is to uncover patterns that may be useful for finding roots for a variety of quadratics.

Quadratics in the xb Plane

In the previous exploration, we looked at quadratics in the standard and vertex form. We also explored changing the different parameters and the graphical effects. We will now look at these same quadratics, but in the xb plane. To do this we will first consider the equation .

Graphed in the xb plane we have the following (note that the parameter a will remain at 1).

 

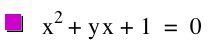
Varying C and the Family of Functions

For the constant parameter of c, we can vary the graph in the xb plane by looking at positive and negative values. First we will explore the positive values of c.

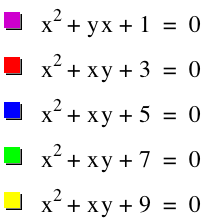
When c=0, we have a straight line at x=-b and a straight line at x=0. Last we will look at negative values of c.

When we put our varying values of c together on one graph, we have a family of hyperbolas.

 

Finding Roots

The emphasis on this exploration is that we do not want to find roots through common procedural methods. When looking at quadratics in the xb plane, we can plot horizontal lines (b=c where c is some constant) and find the intersection points.

Again consider in the xb plane. The number of times the horizontal line b=c intersects the quadratic will tell us the number of roots. There are no real solutions whenever |b|<2 , one real solution when |b|=2 and two real solutions whenever |b|>2. We can validate our pattern assumptions by analyzing the quadratic formula. When b=2 or b=-2, the quadratic formula will give us one root of -b/2. When |b|<2, the discriminant will be negative and this will give us no real solutions. When |b|>2, the discriminant will be positive and this will produce two real solutions.

RETURN