The Standard forms of a Parabola and an Inquiry into Their Interrelatedness

by: Al Byrnes

Show and describe the relationship between these two forms of the graph of a parabola:

y = ax² + bx + c (standard form)

y = a(x - h)² + k (vertex form)

Show the derivation of one equasion from the other and give an interpretation for the value of the parameters a, b, c, h, and k.

Part 1: show the derivation of the standard form of a parabola from the vertex form for a parabola:

y = a(x - h)² + k

= a((x - h)(x - h)) + k

= a(x² - hx -hx + h²) + k

= a(x² - 2hx + h²) + k

= ax² - 2ahx + ah² + k

= ax² + (-2ah)x + (ah² + k)

Let b = (-2ah) and c = (ah² + k)

So after substitution: y = a(x - h)² + k = ax² + bx + c

What is the relationship between the different parameters in the two standard forms? Lets begin the discussion with a reminder of the meaning of the parameter values h and k, from the vertex form of the parabola. h and k are the x and y coordinates of the parabola's vertex, respectively. The graph below provides an illustration of the parabola y = (x + 1)² + 1 (vertex form)

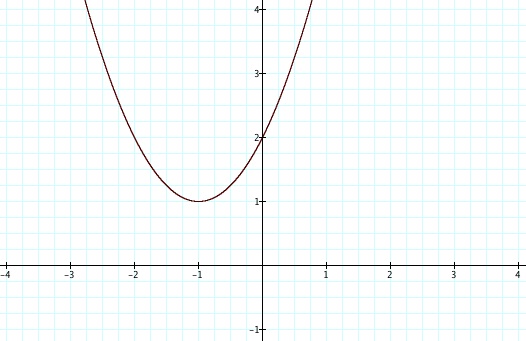
Note that if we consider the general vertex form of the parabola y = a(x - h)² + k with the parabola sketch above, we can confirm that the vertex is at (h, k) or (-1, 1) as expected. Also note that in our example, the value of the parameter a is 1.

Using the relationships established above, let's try to determine coeffiecents c and b to be used in the standard form of the equasion for the same parabola:

b = (-2ah); c = (ah² + k)

To determine the value of parameter c for this example, let's plug in the values for the parameters a, h, and k from our example, where a = 1, h = -1, and k = 1:

c = (ah² + k); c = (1•(-1²) + 1)

c = (1•1 + 1)

c = (1 + 1)

c = 2

The number two is also significant when considering the graph of our parabola y = x² + 2x + 2 or y = (x + 1)² + 1; how is the value 2 pertainate to the graph below?

The value of the parameter c appears to correspond with the value of the y-intercept of the parabola's graph. Said another way, a parabola will intersect with the y-axis at c = (ah² + k). This is pretty cool as we can see from this equasion how the leading coefficient a, and the x and y coodinates of the vertex (h and k, respectively) are multiplied and added to determine the y - intercept of the parabola.

Nice. What about the parameter b from the standard form of the parabola? Recall that we determined by algebraically manipulating the vertex form of the parabola that the value of parameter b could be determined as a product of the leading coefficient, the x coordinate of the parabola's vertex and -2. So let's try it out. Given our vertex form and the parameter values extracted from that vertex form, here are the necessary steps to finding the value for parameter b:

vertex form of parabola: y = (x + 1)² + 1

b = (-2ah); a = 1, h = -1

b = (-2•1•(-1))

b = 2

Here we can see how the parameters a, h, and -2 influence the value of the parameter b in the standard form of a parabola.

We have additionally ascertained the values of a, b, and c necessary for representing the parabola expressed in vertex form in standard form:

y = x² + 2x + 2

Write up 2: part 2. Give an interpretation for the value of the parameters a, b, c, h, and k.

To be continued...

Return to top

Return to my student page