Roots of Quadratic Equations, Their Relationship to Parameter Values, and a Cubic Extension

by: Al Byrnes

In this write up, we will try to examine some patterns for roots and how these roots are related to the values of the parameters a, b, and c in the quadratic equation. Then extensions will be suggested for further investigations using these observations.

To begin, consider the equation x² + bx + 1 = 0 in the xb plane. The graph of this equation is shown below; the horizontal axis is the x-axis while the verticle axis represents the b-axis:

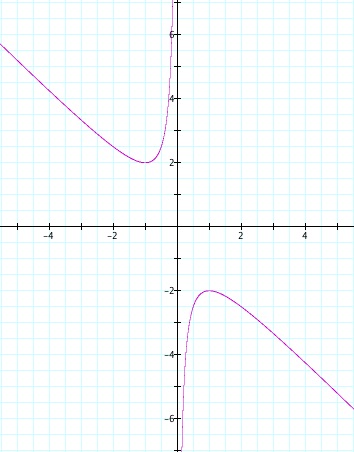
If we graph different values of the parameter b as lines in the xb plane we can obtain some interesting information about the number of real roots for the quadratic equation x² + bx + 1 = 0 and information about the sign of those roots. For instance, if we choose b = 2, the equation will have a single negative root:

x² + 2x + 1 = 0; what values of x satisfy this equation?

If we factor this quadratic equation we will obtain x² + 2x + 1 = (x + 1)² = 0; so there is one root for this quadratic equation, whose value is x = -1. But how does this result correspond to the graph of x² + bx + 1 = 0. More importantly, can we develop a pattern to help improve our intuition about the number and signs of the roots of a quadratic equation based on the values of a, b, and c.

Well, lets just consider x² + bx + 1 = 0. We determined that when b has the value of 2, there is one negative root with the value x = -1. In the plane these two equations graphed together look like this:

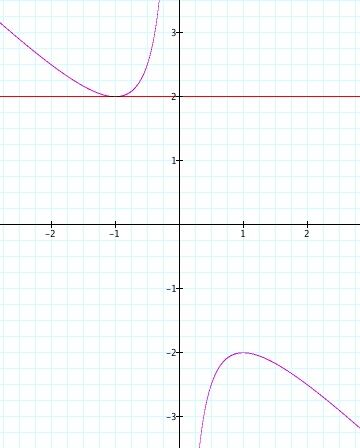
Note the point at which the line b = 2 and the graph of the quadratic equation x² + bx + 1 = 0 are cotangent. The graphs of the two equation are cotangent at a single point, which is very interesting considering that, when we solved the equation above, we found a single root. This roots value, x= -1 can also be represented in the plane as the point of cotangency between the line b = 2 and the equation x² + bx + 1 = 0 as the ordered pair (-1, 2).

So, our intuition might suggest that the number of real roots will correspond to the number of times the line b = a (where a is a real number) intersects the curve x² + bx + 1 = 0. Furthermore, the values of the x coordinate of the order pairs that indcate the points at which these two curves intersect should indicate the values of the roots of the equation x² + bx + 1 = 0. Let's test this intuition. Consider the quadratic equation x² + bx + 1 = 0 and the line b = 3.

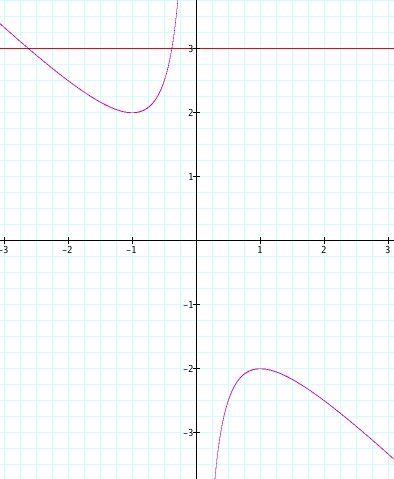
So, now we have a situation in which out intuition might suggest that the quadratic equation x² + 3x + 1 = 0 has two real roots, each with a negative value. Using the graph, let's make an initial guess for the values of the roots: I would guess x = -2.62 and x = -.382. These guesses were obtained using the Graphing Calculator:

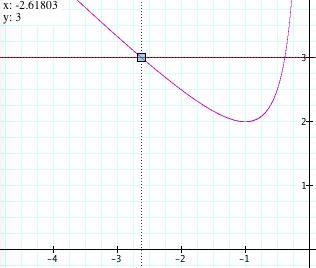
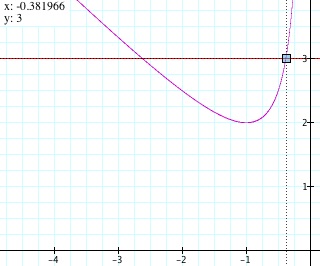
As a check, let's use the more conventional method of obtaining the value of the roots of a quadratic equation more "resistant" to an easy factorization, the quadratic formula:

x = (-3+√(5)/2) and (-3-√(5)/2)

Indeed after calculation, these values match up with those values we predicted for the roots! In an examination of other values for the line b = a we can continue to firm up our assumptions. Consider the line b=0 and the quadratic equation x² + bx + 1 = 0. Based on the graph of these two curves in the plane and points at which they are coincident, what assumptions could we make about the number and signs of the real roots of the equations?

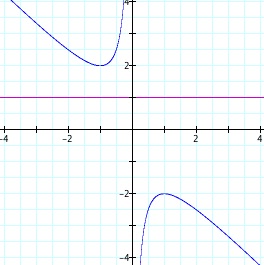
I would venture a confindent guess that the quadratic equation x² + x + 1 = 0 has no real roots, in large part because the curves x² + bx + 1 = 0 and b = a; 2 > a > -2 are not coincident along the range 2 > a > -2. In fact, once we employ the quadratic formula we do see that x² + 1x + 1 = 0 has no real roots:

x = (-1+√(-3)/2) and (-3 - √(-3)/2). Again, our intuition was correct!

Let's check two more values of b to finalize our strategy for making obserations concerning the values and number of real roots of quadratic equations. The final two values of b that we will graph will be the lines b = -2 and b = -3.

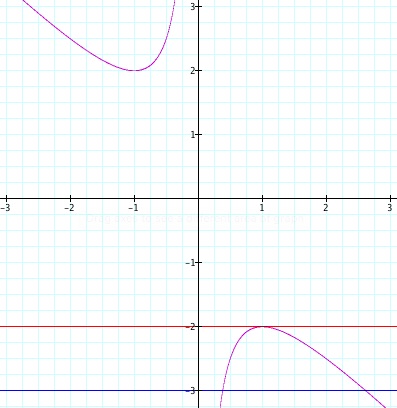
The line b = -2 is indicated in red while the line b = -3 is indicated by the blue coloring. Indeed we can see when comparing the graph and the intuition we developed, that the quadratic equation x² + -2x + 1 = 0 and the equation x² + -3x + 1 = 0 have one positive real root and two positive real roots, respectively. For algebraic justification, see below:

x² + -2x + 1 = (x - 1)² = 0; real root: x = 1

Using the quadratic formula to obtain the roots for x² + -3x + 1 = 0:

x = (3+√(5)/2) and (3 - √(5)/2), indicating that there are two, positive real roots.

Can we extend these observations to equations of higher degrees? Let's examine a cubic expression of the following form:

We will be specifically interested in the case when b = -2 for this investigation.

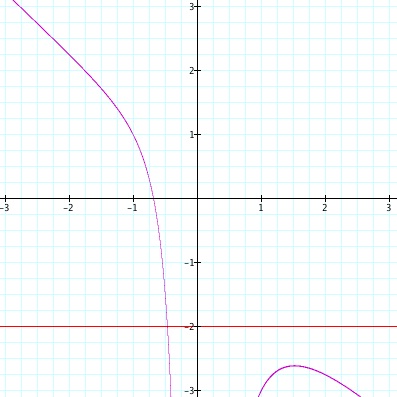
Using the intuition we formed with regards to what the intersection of these two curves can tell us about the real roots of a quadratic equation, let's extend out thinking to the graph of the cubic expression shown above x³ + -2x² + x + 1 = 0. My initial guess would be that the expression has 1 real root with the x value of the order pair that describes the point at which the line b = -2 and the curve x³ + -2x² + x + 1 = 0 are coincident. Using Graphing Calculator, we are able to determine the value of this point with relative accuracy:

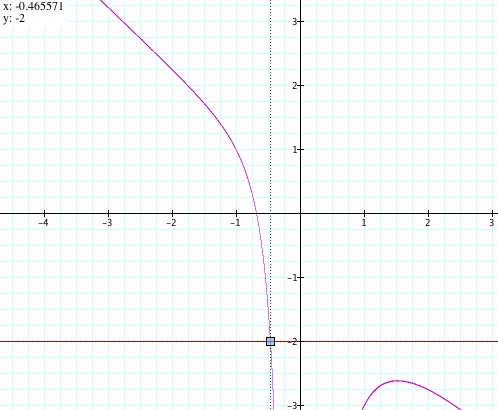
So the value of this root is appromately -.465571. Let's do a check using some algebra:

x³ + -2x² + x + 1 = 0

x(x² - 2x + 1) = -1

x(x - 1)² = -1

x(x - 1)² - 1 = 0

Let x = -.465571

(-.465571)((-.465571) - 1)² - 1 = 0

After the calcuations are completed we see that taking error brought on by rounding into account, the value -.465571 satisfies the equation and is therefore very near the value of the actual real root of the cubic equation!

Return to top

Return to my student page