Write-Up #1 (Graphs)

x⁵ = (x² - y²)(x² - ay²)

By Jaepil Han

12. Explore the equation at the right for different valvues of a.

x⁵ = (x² - y²)(x² - ay²)

 

Here's the graph of the following equations when a varies from 1 to 5

         

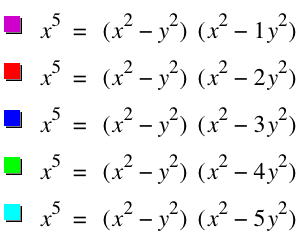
The part of the graph in the second and third quadrants has sort of "ribbon" shapes. When the value of a is getting bigger(from 1 to 5), this ribbon shape is getting bigger, or far from the origin. Also, the part of the graph in the first and fourth quadrants is getting narrower than the previous when the value of a is getting bigger.

Here's the graph of the following equations when a varies from -1 to -5.

         

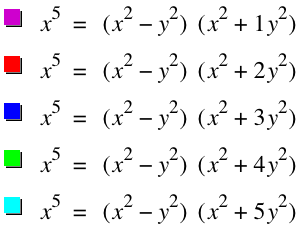
The graph of these equations has sort of hearts shape. When the value of a is getting smaller(from -1 to -5), the heart has bigger "ears," or is getting far from the origin. Although the graphs may change their shapes, the intersections of the equations and the x-axis are the same as 0 and 1. Algebraically, the x-intercepts are the points when the y value is zero. Thus, substitute 0 as a value of y. Here's the equation.

x⁵ = (x² - y²)(x² - ay²)

x⁵ = (x² - 0 )(x² - 0 )

x⁵ = x⁴

x⁵ - x⁴ = 0

x⁴(x- 1) = 0

Thus, x = 0 or 1 as expected.

 

Here's a movie file when the value of a varies from -5 to 5.

Here's an interesting point. There is only one point that all the graph of the equation is completely in the first and fourth quadrants.

 

When a=1,

x⁵ = (x² - y²)(x² - y²)

x⁵ = (x² - y²)²

Since the rigrt side of the equation (x² - y²)² is always non-negative value, x⁵ shuold be non-negative also. Thus, the value of x is non-negative. Therefore, this is a reason why the graph of the equation x⁵ = (x² - y²)(x² - y²) lays totally on the first and fourth quadrants.

 

Return to Jaepil Han's Page

Return to EMAT 6680 Page