

Write-Up #2 (Quadratics)
y = ax2+bx+c
By Jaepil Han
Problem 2. Fix the values for a and b, vary c. Make at least 5 graphs on the same axes as you vary c.
y = ax2 + bx + c
We want to focus on the patterns when the values of parameters a, b, and c vary. Here's the standard form of quadratic functions.
y = ax2+ bx + c
The pattern of the quadratic equation when the values for a and b are fixed and the value for c varies from 3 to -3.
Here's the graphs using the Graphing Calculator.
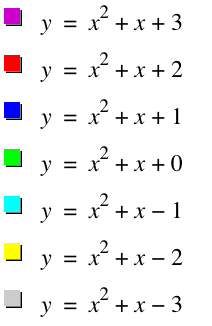
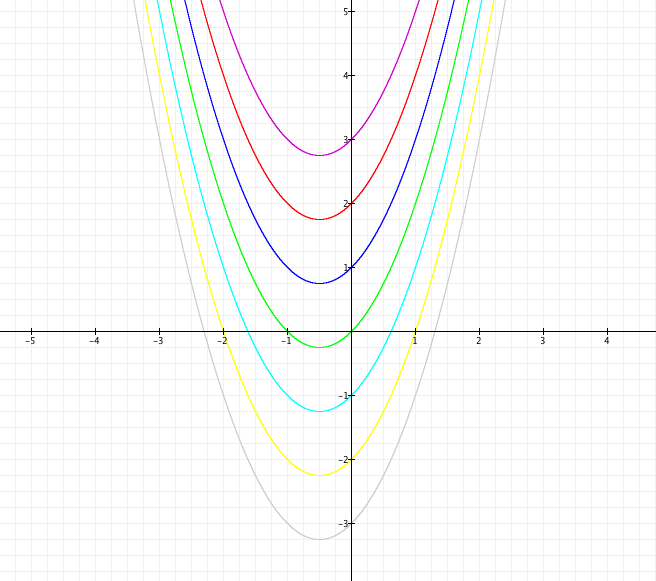
When the parameter c varies from 3 to -3, the graph of the equation is vertically translated. Also, as you may noticed, the y-intercept of the equation is the same as the value of c. For example, the y-intercept of y = x2+ x + 3 is 3 and that of y = x2+ x - 1 is -1.
Also, here's the animation of the graphs when the value of c is varied from +5 to -5.
At this point, it seems that the pattern of the quadratic function when only the value for c varies is vertical translations of one of the quadratic functions. Or, we can express all those graphs are the translations of the quadratic equation y = x2+x+0.
We might prove this is a translation by mapping. Since our students are not familiar with mapping stuff, we simply introduce it as a dilation of the quadratic equation y = x2+x+0.