Transformations of Quadratic Functions

by David Henderson

 

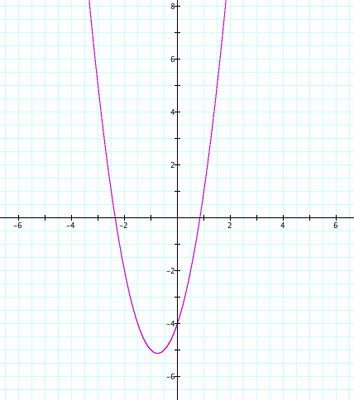
We begin by taking a look at the graph of  y = 2x2 + 3x - 4,  shown below:




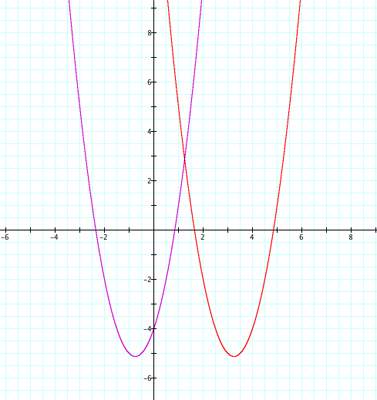
(This function is in standard form, that is, in the form  y = ax2 + bx + c, where a, b and c are real numbers.) 

Now, let's replace x with (x - 4), giving the function  y = 2(x - 4)2 + 3(x - 4) - 4,  and look at the change to our original function:

Replacing x with (x - 4) results in a translation of the original graph 4 units to the right.



Suppose we would like the vertex to be in the second quadrant. We could accomplish this by translating our original function to the left, and up. This can be accomplished as seen in the graph below using, for example, the function


y = 2(x + 4)2 + 3(x + 4) + 2


What if we wish to have a graph which shares the same vertex, but opens downward? This can be accomplished by reflecting the original function vertically. In this case, we could use the function


y = - (2x2 + 3x - 4) - 10.25


The negative sign in front of the parentheses will reflect the parabola across the x-axis, then subtracting 4 and subtracting 6.25 wil translate the entire parabola down so that its vertex will be the same as the original parabola. This is the same result as reflecting across the line y = -6.25 (the y-coordinate of the original vertex).

In general, for a quadratic function in standard form  y = ax2 + bx + c, where a, b and c are real numbers,