

Quadratic functions have traditionally occupied a large part of secondary mathematics. Mostly, the emphasis has been on finding the zeros, or roots. That is, given the quadrtic function
,
solve for the values of x that satisfy the quadratic equation
.
If we let a = c = 1, we get the equation
,
which is graphed in the x - b plane below:
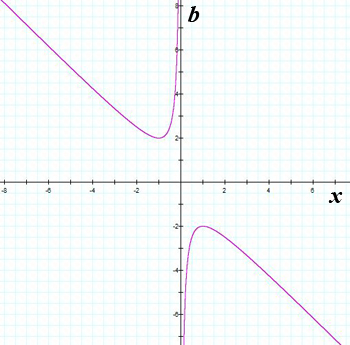
If we set b equal to a particular value, such as 3, and look at the two graphs together, we see that the graph of b = 3 intersects the graph of x2 + bx +1 = 0 at two points. These points correspond to the roots of the quadratic equation x2 + 3x +1 = 0, as shown:
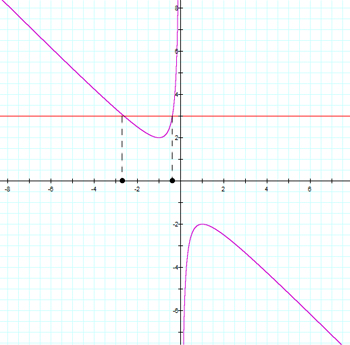
Click here to see an animation of -7 < b < 7. This will show the values of b for which there are 0, 1 or 2 real roots of x2 + bx + 1 = 0.
Notice that for b = 2 there is exactly one negative real root, and for b = -2 there is exactly one positive real root. This is clear, because solving the quadratic equations
x2 + 2x + 1 = 0 and x2 - 2x + 1 = 0
is equivalent to solving the equations
(x + 1)2 = 0 and (x - 1)2 = 0,
respectively, yielding one (repeated) real root in each case. Otherwise, for -2 < b < 2, there are no real roots for x2 + bx +1 = 0, and for b > 2 or b < -2 there are 2 real roots.
In the case above, we fixed the value of c at 1. The following illustration shows a family of hyperbolas formed in the x - b plane by letting c = 1, 3, 5, 7, 0, -1, -3, -5, and -7.
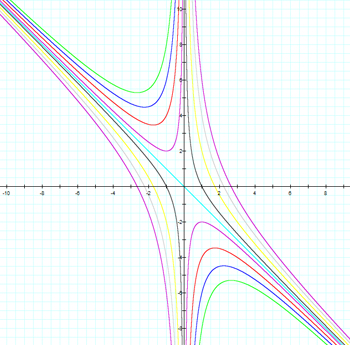
For c = 0 , we get the asymptotes for all of the hyperbolas. Otherwise, for c > 0 , varying the value of b as before, we have 0, 1 or 2 real roots as given by the intersection of the graph of b = n and the graph of the particular (vertically oriented) hyperbola for the given value of c.
For c < 0 the function will have 2 real roots, as given by the intersection of the graph of b = n and the graph of the particular (horizontally oriented) hyperbola for the given value of c.