

In this exploration we will investigate some interesting polar graphs and explore their mathematical propeties. We begin with the following:

Curves of the form r = aθ are known as the Spiral of Archimedes. These curves are all similar. Changing the value of a dilates the curve. The curves above are shown with 5 revolutions (0 < θ < 10π). The terminal side of any angle, θ, in standard position is partitioned into equal segments by the spiral.
Next, we examine the following graph:

At first glance, the graph appears to be a line. However, the function is undefined when sin θ = cos θ, so this graph is a line, but with holes at π/4 +/- nπ, n = 1, 2, 3, ... . Due to the way Graphing Calculator 4.0 renders the graphs, and the pixel dimensions of the screen, we are not able to see these holes. Also, no matter what the screen resolution or pixel dimension used, a single point, having no size, would never be rendered by the program anyway.
Next, we examine the following family of graphs:


As in the previous example, these polar functions are undefined where sin(nθ) = cos(nθ), n = 2, 3, 4, ... , so there are holes in each graph for these values of θ. Also, some interesting patterns develop. When the value of n is even, the asymptotes form a regular (2n)-gon centered at the origin, and the graph has 2n branches. When the value of n is odd, the asymptotes form a regular n-gon, also centered at the origin, and the graph has n branches.
Click here for a larger view.
Click here for animation for n = 1, 2, 3, ... , 18.
Now, let's take a look at the following graph:
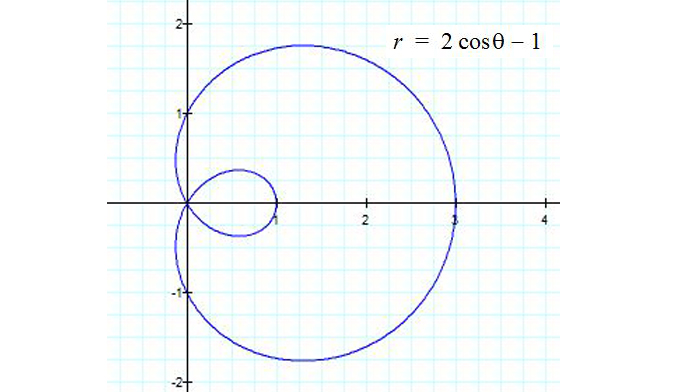
This curve is known as the Limaçon of Pascal. Generally, the polar equation is
The Limaçon of Pascal was discovered by Étienne Pascal (father of Blaise Pascal) and named by another Frenchman Gilles-Personne Roberval in 1650 when he used it as an example of his methods of drawing tangents (i.e. differentiation).
The name limaçon comes from the Latin limax meaning 'a snail'. Étienne Pascal corresponded with Mersenne, whose house was a meeting place for famous geometers including Roberval.
Dürer should really be given the credit for discovering the curve since he gave a method for drawing the limaçon, although he did not call it a limaçon, in Underweysung der Messung, published in 1525.
When b = 2a the limaçon becomes a cardioid, while if b = a it becomes a trisectrix. Notice that this trisectrix is not the Trisectrix of Maclaurin.
If b ≥ 2a the area of the limaçon is (2a2 + k2)π. If b = a the area of the inner loop is a2(π - 3√3/2), and the area between the loops is a2(π + 3√3).
The limaçon is an anallagmatic curve.
The limaçon is also the catacaustic of a circle when the light rays come from a point a finite (non-zero) distance from the circumference. This was shown by Thomas de St. Laurent in 1826.
To derive the Cartesian equation for this curve, we use the facts that a and b are parameters,
Thus, the derivation of the Cartesian equation is: