


Here is the graph of y = 2x² + 3x - 4 :

Considering what we know about the general equation for a parabola, y = ax² + bx + c, and the possible transformations depending on values of a, b and c, we can discuss this graph. We know it will open up because a is positive. The y intercept is c, which is (0, -4). Our x intercepts are the two values we get when y is set equal to zero and we solve for x. For this particular graph, I can easily retrieve the values of x for the intercepts by clicking on those points when I graphed it in Desmos. The values were x = -2.35 and x = .85, so the points of our x intercepts are (-2.35, 0) and (.85, 0). We can find the x and y values of our vertex the same way, which is the point (-.75, -5.13). With a general equation of a parabola, there are algebraic ways to find all of these key points of our graph, but that is much easier to do if the quadratic that gives us our parabola is easily factorable, which in this case it is not.
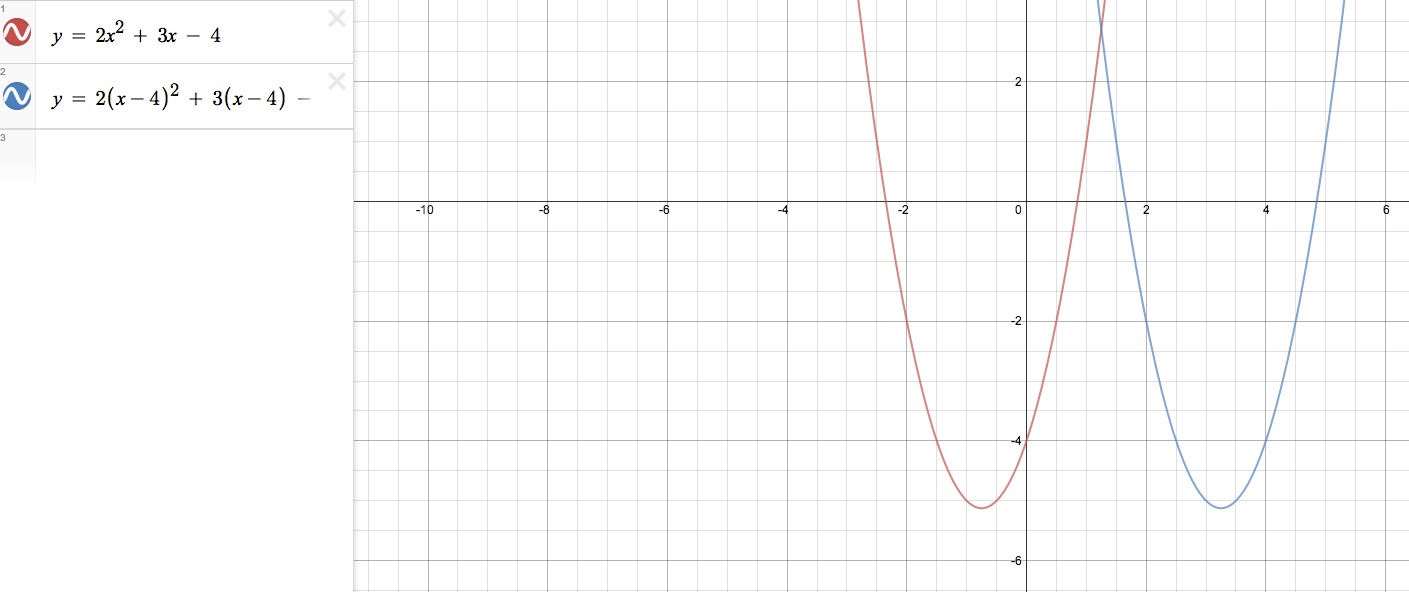
i. Overlay a new graph by replacing x with (x-4)
Now we see here that by replacing x with (x-4), the parabola has shifted to the right.
ii. Change the equation to move the vertex of the graph into the second quadrant.
Now looking back to our original graph shown in red that we have plotted in the first part, it's vertex currently lies in the 3rd quadrant of our coordinate system. So, to move it into the second quadrant, we can modify our equation. Considering the standard equation of a parabola, y = ax² + bx + c, we know that c is our y intercept, which in this particular case is -4. By changing our equation to make this +4, we have successfully moved our vertex from the 3rd to the 2nd quadrant. You can see the slightly different equation change in the picture below.
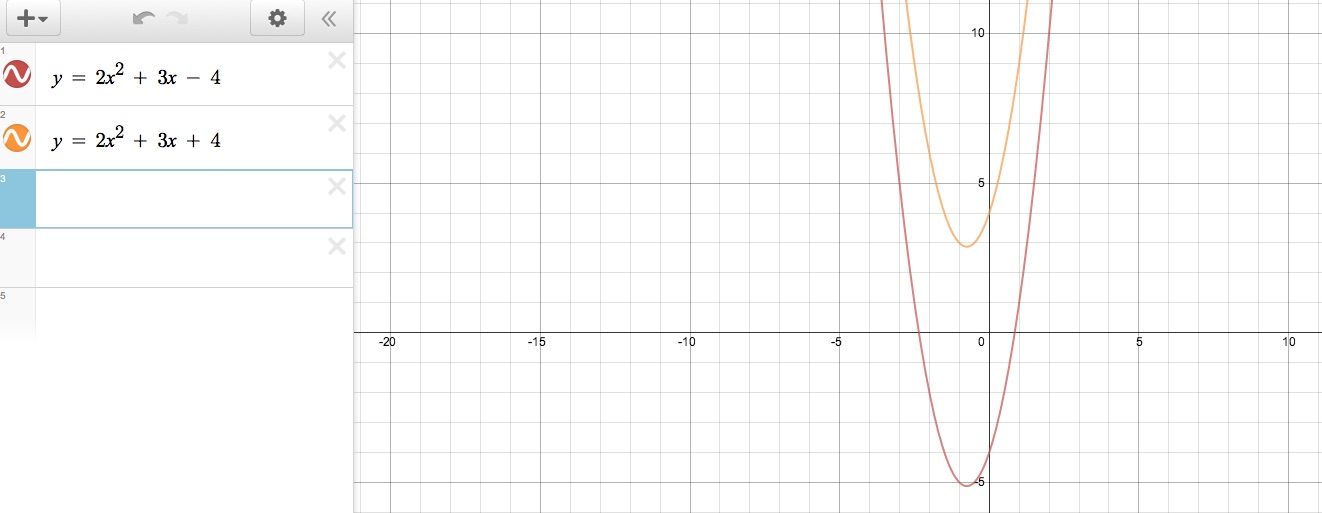
Further, we can justify this moving of the vertex algabraically. The vertex is usually given as (h, k) where h is found using h = -b/2a for when the equation of the parabola is given in standard form rather than vertex form. So, using y = 2x² + 3x -4, we see that h = -3/4, or in other words, our x value of our vertex. Then, we plug this value back into our equation to get k, or our y value of our vertex, which would give us -5.125. So our vertex is (-.75, -5.125). In order to move it into the second quadrant, all we really care about is making the y value of our vertex positive. So, by changing the c value to +4, our x value of our vertex stays the same because h is only found using values a and b. However, when we plug -.75 back into our new formula of y = 2x² + 3x +4, our y value of our vertex is now positive. Therefore, our vertex has shifted up from the 3rd to the 2nd quadrant.
Another method for working with the vertex would be to take our parabola given in standard form and convert it to vertex form, which would allow us to find the values of our vertex directly from the formula. The general vertex form of a parabola is given by y = a(x-h)² +k, where again, our vertex is given as (h, k). So it's easy to see how to get these x and y values (h and k) of our vertex directly out of vertex form because those variables already exist. So, let's take our original parabola, y = 2x² + 3x - 4 and complete the square:
2(x² + (3/2)x) = 4
2(x² + (3/2)x + 9/16) = 4 + 18/16
2(x+3/4)² = 82/16
y = 2(x + .75)² - 5.125 is our parabola now given in vertex form. Therefore, we can say h = -.75 and k = -5.125, so our vertex is (-.75, -5.125) as expected.
Now, to modify this formula, all we have to do is simply change our k value from negative to positive so that the vertex is changed from a negative y value to a positive y value, and therefore, translated from the third to the second quadrant as desired. See the picture below with the graphs plotted using our new equations in vertex form rather than standard form.

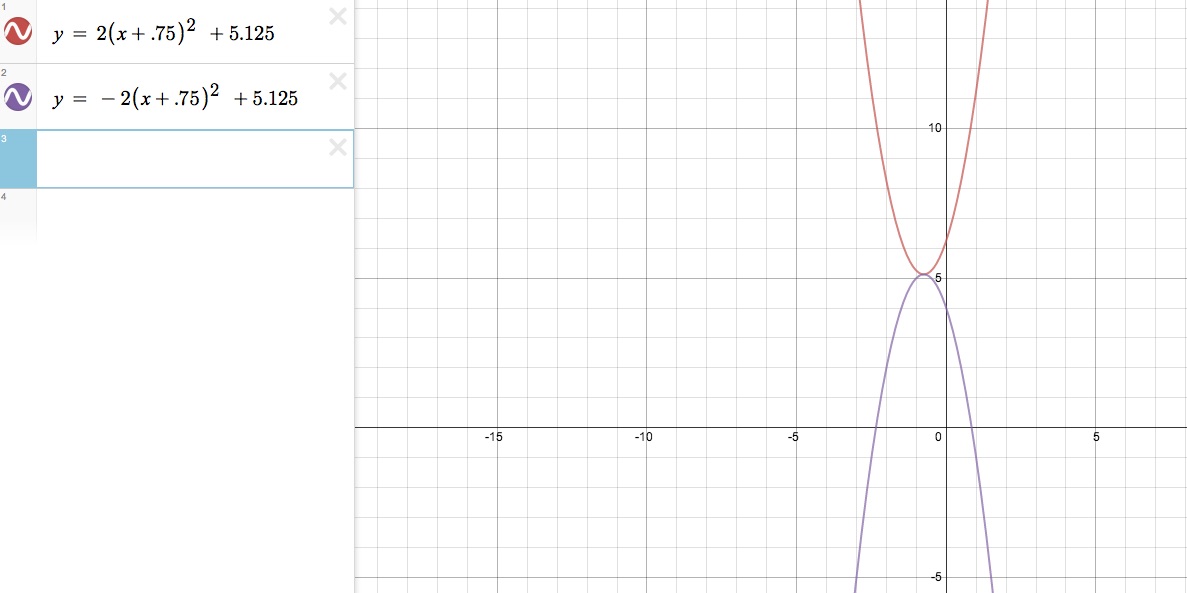
iii. Change the equation to produce a graph concave down that shares the same vertex.
Now we are asked to make another transformation with our parabola: make it concave down. In other words, we want to flip it, but keep the same vertex. To make this easiest, we will still consider the equation in vertex form. Let's also work with the parabola that we just translated into the second quadrant, so the equation of the graph that we're working with is y = 2(x + .75)² + 5.125. We want the same vertex, so h and k must stay the same. Our transformation now depends on changing the value of a from positive to negative to flip the parabola and make it concave down. In this case, a = 2, so our new equation should be y = -2(x + .75)² + 5.125 to get our graph concave down.
iv. Generalize...
So to me it seems that working with transformations of parabolas is much more easily done if our equation of the graph is given to us in vertex form. So again, the general vertex form is y = a(x-h)² + k. The value of a shrinks or stretches how open our parabola is and a positive a will produce a parabola that opens up, while a negative a value will produce a parabola that opens down. The vertex of our parabola is found using the values of h and k in the form of a point (h, k). If you're given the equation of a graph in standard form, or quadratic form as we were at first in this investigation, you can convert it to vertex form by the process of completing the square.
Return to Home Page