


In the image above, these are different graphs for the quadratic equation ax² + bx + 1 = 0 where the values of a and b are being changed to create translations of the original graphs. However, it is important to note that these don't appear as regular parabolas as expected because they are graphed in the xb coordinate system. So x is the horizontal axis and b is the vertical axis. In the image above, the equation 2x + b = 0 has already been added and is the diagonal line seen in purple. So, as stated above, the intersection of any horizontal line wiht 2x + b will occur at a point midway between the intersections with each of the hyperbolas.
Let's first relate 2x+b = 0 to our original quadratic x² + bx + 1 = 0 before moving onto its relation to the quadratic formula. x² + bx + 1 = 0 is the quadratic that gives us the hyperbolas that our line is going through. Well, interestingly enough, the derivative of the quadratic equation x² + bx + 1 = 0 is indeed 2x + b = 0. If we solve this derivative for x, this gives us a root of our graph.
Now, we want to discuss this line's relation to the quadratic formula:
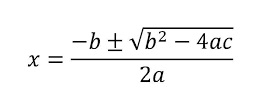
Because we have kept the traditional x axis as the horizontal axis the same, when finding the zeros or roots of our quadratic function, they are still given in terms of x. When given any quadratic equation, you can use the quadratic formula to find that particular equation's roots. If you notice the plus or minus symbol in the quadratic equation, this implies that you will be given two different values for x, or in other words, two roots. Depending on the particular quadratic you are plugging into the formula, the values of your result will either give you two real roots, one real root, or two imaginary roots.
Now in our particular situation, we already discussed that 2x+b = 0 being the derivative and solving this for x will give us a root. We use the quadratic formula to find roots of a quadratic as well. Therefore, the intersection of 2x + b = 0 with any of the hyberbolas gives us the two roots of our equation because it intersects at two points. So further, if we draw a hortizontal line to intersect with 2x+b, it will occur halfway between the two roots.
Return to Home Page