by Courrey J. Alexander
This is an exploration of the graph:
x=cos(at)
y=sin(bt),
for various values of a and b.
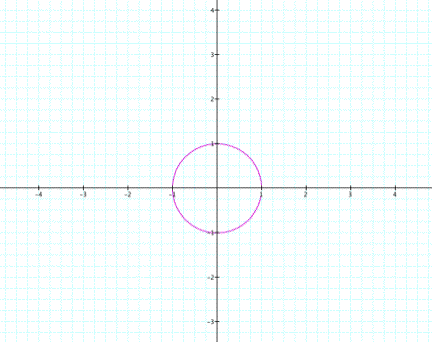
When a = b, as a and b
increase, we eventually get a circle with radius of 1 starting at (1,0) and
moving in a counterclockwise direction. Click here to see the behavior of the graph.
When both a and b are negative
the same graph appears (a=b) except the graph of the circle moves in the opposite
direction.
Next, we will examine the parametric
equations:
a cos t
b sin t, for various values.
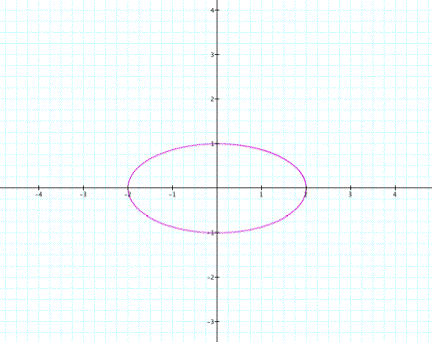
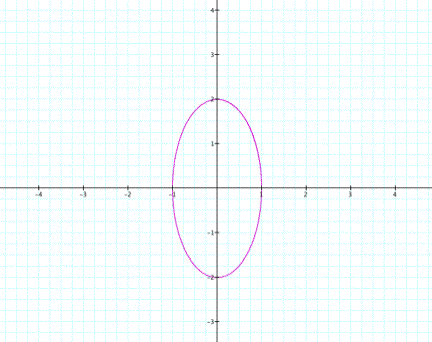
First let's look at when a=2 and b=1, and
when a=1 and b=2.
With these graphs, we can see here that we no longer have circles, but we have ellipses. Click on the graphs to see the behavior of each respective graph.
LetÕs examine the graphs of parametric
equations:
x=cos(at)
y=sin(bt), for various values when a does not
=b.
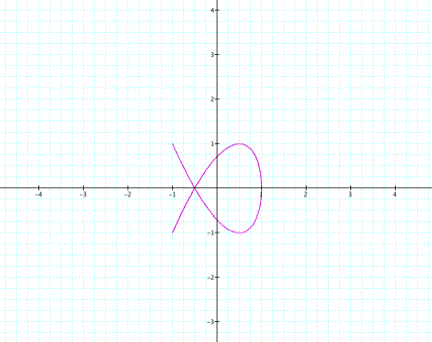
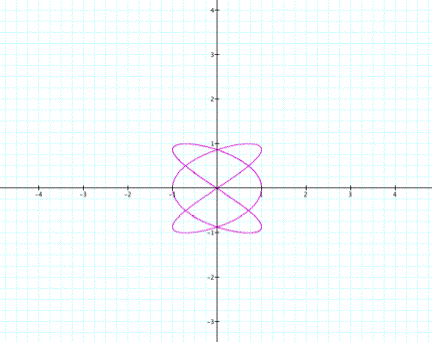
The first graph is symmetric across the x-axis. The second
graph is symmetric across
both axes. Will the graph change if the values of both a and b are
negative?
What happens when sin and cos are
transposed?
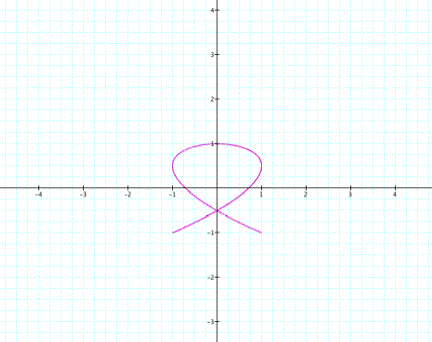
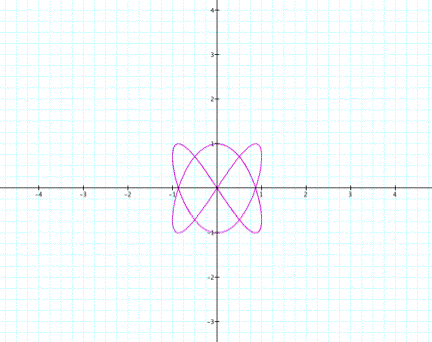
The first graph is now symmetric across the y-axis. The second
graph remains symmetric
across both axes.
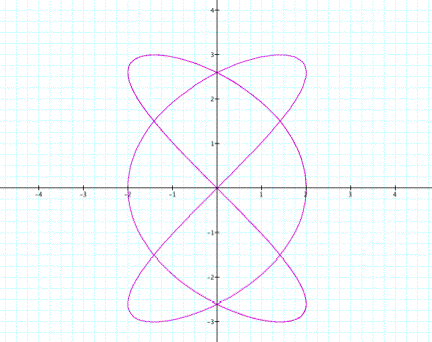
Our final investigation takes a look at what
happens to the graphs of the parametric equations when a and b change and the
coefficients of cos and sin change?
HereÕs a look at a sample graph.