by Courrey J. Alexander
Graphs in the xa plane.
First, letís consider the
graph of the equation y=ax2+x+1. Since we are looking at graphs in the xa plane, we need to
consider the graph of the equation ax2+x+1=0. This way we can identify all roots for
a . Hereís the graph for the
equation.
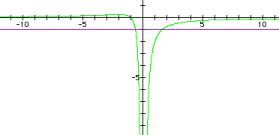
Here the equation will have
one, real negative root at a=0.
When a is between 0 and
approximately 0.25, the equation will have two, real negative roots. When a is less that 0, then the
equation will have two roots (a positive and a negative). There arenít any real roots when a is
greater than 0.25.
Letís look at the graph of
y=x2+bx+1 for -3£b£3.
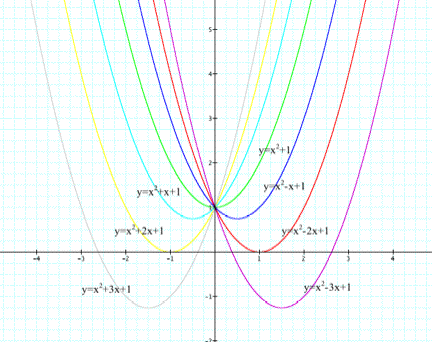
The graph of the parabola is translated
upward from the right until the axis of symmetry is at 1. Then the graph is translated
downward. The parabola always
passes through (0,1) on the y-axis.
When b=2,-2, the equation has one real negative and one real positive
root, respectively. When b<-2, the equation has two real, positive roots. When b>-2, the equation has two real, negative roots. For any value of b between 2 and
–2, the equation has no real roots.
If we consider the locus of
the vertices of the graph above, we can see that it forms a parabola that opens
downward (y=-x2+1).