
by Courrey J. Alexander
Given an arbitrary circle and line, choose an arbitrary point on the line, P. Construct the two tangent circles to the line at P and the circle.
Where to begin? Start with what we know.
1. The center of one of the tangent circles has to lie on the line that passes through the center of the given circle and point P.
2. We need to find a point on this particular line that is equidistant from point P and the given line.
Here’s the beginning of the construction!
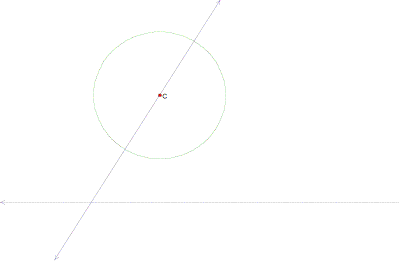
Next, we will construct the perpendicular to the given line which passes through the center of the given circle and label the intersection of said perpendicular and the given circle (point A).
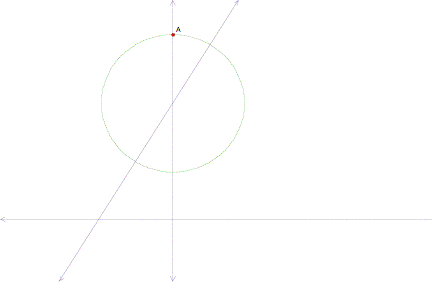
If we construct the line that passes through point A and point P (point B), then we have constructed an isosceles triangle (DCAP). The distance from A to C equals the distance from C to P. Therefore, we know for sure that C is the center of the given circle.

The intersection of the perpendicular from point B to the given line (point D) should give us the center of one of the tangent circles. Just as in the previous construction where we constructed an isosceles triangle (DCAP), we have constructed DDBP. The distance from P to D equals the distance from B to D. Therefore, we know for sure that D is the center of one of our tangent circles.
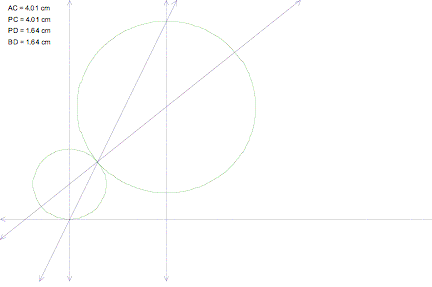
Again, using the same process, we will construct perpendiculars and use intersections to construct another isosceles triangle so that we can find the center of the second tangent circle.
First, we need the line that passes through point P and intersects the circle at the point (point R) where the perpendicular to the given line passes through the center of the circle.
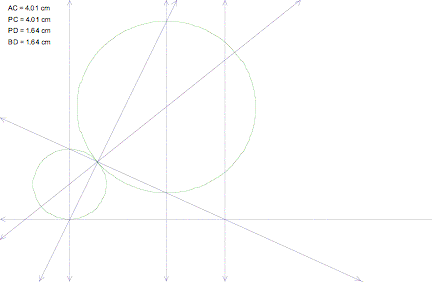
Hence, we have the intersection of this constructed line and the given line, point S. Constructing a perpendicular to the given line at point S gives us another intersection, point T. Just as in the previous two constructions where we constructed DCAP and DDBP, we have another isosceles triangle, DTPS. The distance from T to P equals the distance from T to S. Therefore, we know for sure that T is the center of our second tangent circle.

Click here to view the GSP file.