by Courrey J. Alexander

PETAL TRIANGLES

Construct a triangle, ABC, and choose an arbitrary point, P, in the plane.

Construct the perpendiculars to each side of the given triangle from point P. Label the points of intersection points E, F, and G.

Connecting points E, F, and G, we have the pedal triangle for point P.

Let’s investigate the possibilities as P is translated!

Here, P is the centroid of triangle ABC.

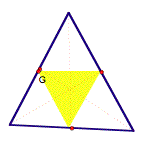
The vertices of the pedal triangle lie on the sides of triangle ABC.

Here, P is the incenter of triangle ABC.

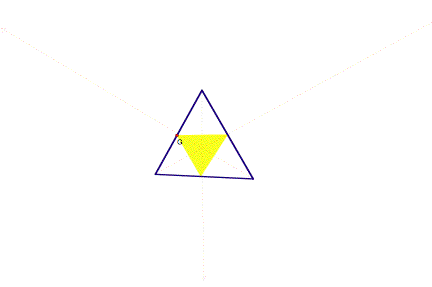
The vertices of the pedal triangle lie on the sides of triangle ABC when P is the incenter as well.

Here, P is the orthocenter of triangle ABC.

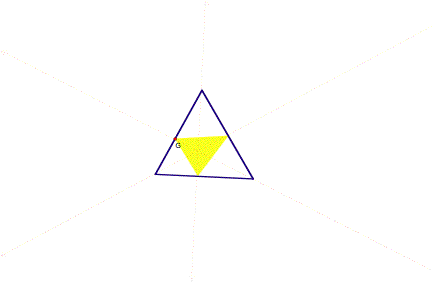
Here the orthocenter is outside of the triangle.

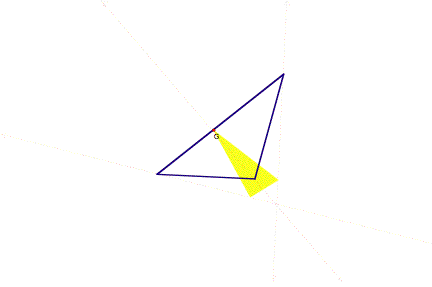
Regardless of where the orthocenter lies (inside or outside the triangle), the vertices of the petal triangle remain on the altitudes of triangle ABC.

What happens when point P lies exactly on one of the vertices of the original triangle? What happens to the petal triangle then? Click here to see.

Return to Homepage