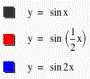Explore Sine Curves y = a sin (bx+c)

From Physics Perspective

Najia Bao

In physics, a sine wave is the image of the graph of the sine function under a composite of translations and scale changes. The higher pitched the sound, the shorter the period of its wave. The louder the sound, the greater the amplitude of its wave. Variations in period or amplitude can be derived from horizontal or vertical scale changes, respectively, of the parent sine function y = sinx.

Problem 5

Now we use Graph Calculator to examine graphs of y = a sin (bx+c) for different values of a, b, and c.

Vertical scale change. Suppose that b = 1, c = 0, and a is a variable, that is, y = a sinx, and let a = ½, 1, and 2 respectively, then we get y = ½ sinx, y = sinx, and y = 2sinx respectively (see fig. 1).

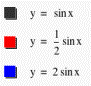
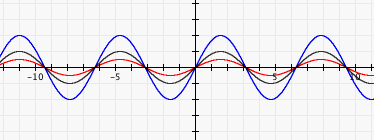
Figure 1

We find that the scale change above is a vertical scale change. If the graphs above represent sound waves, then the function y = 2sinx represents a sound 2 times as loud as the represented by y = sinx. Thus vertical scale changes affect the amplitude of a wave. Similarly, let a = -2, -1, and -1/2 respectively, then we get y = -2sinx, y = -sinx, and y = -1/2sinx, and their graph respectively, which reflects the graph of y = 2sinx, y = sinx, and y = 1/2sinx over x-axis respectively (see fig. 2).

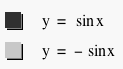
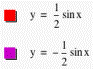
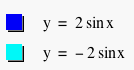
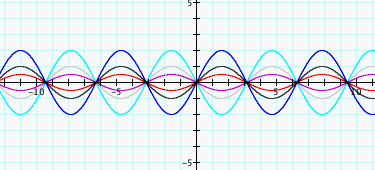
Figure 2

Horizontal scale change. Horizontal scale changes affect the period. Suppose that a = 1, c = 0, and b is a variable, that is, y = sinbx, and let b = ½, 1, and 2 respectively, then we get y = sin½x, y = sinx, and y = sin2x respectively (see fig. 3).

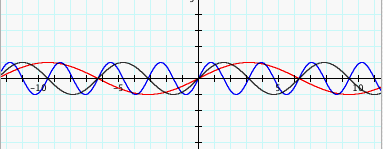
Figure 3

In figure 3, we find that y = sin2x has the same amplitude as its parent function y = sinx, but the period of y = sin2x is a half of the period of y = sinx, that is, y = sin2x can be viewed as a sound having two times the frequency of the original wave y = sinx. Also, y = sin1/2x has the same amplitude as y = sinx, but the period of y = sin1/2x is two times the period of y = sinx, that is, y = sin1/2x can be viewed as a sound having one half of frequency of the original wave y = sinx.

Let’s go on. We find something interesting that y = 2sin (3x) has the same graph as y = -2 sin (-3x), and y = 2sin (-3x) has the same graph as y = -2 sin (3x) (see fig. 4), that is because the sine function is an odd function. Hence 2sin (-3x) = -2 sin (3x) and -2 sin (-3x) = 2sin (3x).

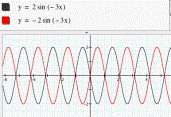
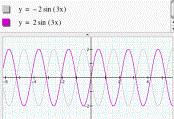
Figure 4

Translation along x-axis. Now let’s further explore the graphs of y = a sin (bx+c). Suppose that a = 1, b = 1, and c is a variable, that is, y = sin (x+c), and let c = -3, -2, -1, 0, 1, 2, and 3 respectively, then we get y = sin (x-3), y = sin (x-2), y = sin (x-1), y = sin x, y = sin (x+1), y = sin (x+2), and y = sin (x+3) respectively (see fig. 5).

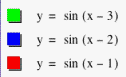
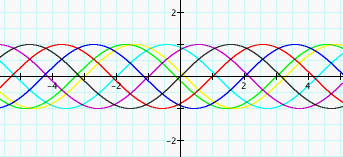
Figure 5

From the figure above, we can conclude that when c = 1, 2, and 3, respectively, y = sin (x +c) translates the graph units left. And when c = -1, -2, and –3, respectively, y = sin (x +c) translates the graph units right.