“The Helen of Geometry”

Explore Cycloids

Najia Bao

Good morning! Everyone. Today let’s investigate and explore the “Helen of Geometry”, that is, cycloid. It was the first time that I heard about cycloid when I was 12 years old. My father, a mechanical engineer who was just designing a kind of system of cycloidal gears, told me the history of cycloid, from Galileo, one of the first people to study the cycloid, to two famous problems about cycloid - Christian Huygens’ tautochrone problem and John Bernoulli’s brachistochrone problem. Also, he explained the difference between cycloidal gears and involute gears and their strength and weakness as well. Frankly, at that time, I was not interested in what he said. However, after I took the course Differential Geometry (during my graduate study), I master knowledge of cycloids.

Problem 12

A cycloid is the locus of a point on a circle that rolls along a line. Write parametric equations for the cycloid and graph it by GSP.

The cycloid is the locus of a point P on the rim of a circle of radius r rolling along a straight line (see Figure 1). Suppose that the circle rolls along the x-axis and one position of P is the origin, let’s find parametric equations for the cycloid.

Now, we view the angle of rotation t of the circle as parameter. As we know, t = 0 when P is at the origin. When the circle has rotated through t radians, the distance rolled is OT = arc PT = rt. Suppose the coordinates of P be (x, y), we get that x = OT – PQ = rt – r sint = r (t - sint), that is, x = r (t -sint). Similarly, we get that y= r (1-cost) (see fig. 1). Therefore the cycloid-the path of the moving point P – has parametric equations x = a (t - sint), y = a (1-cost).

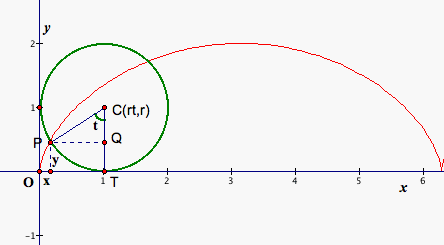
Figure 1

Now we construct the cycloid by GSP.

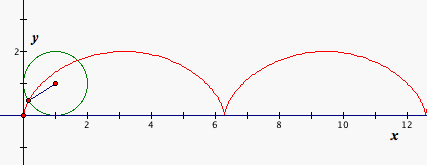
Figure 2

Now let’s further explore cycloids. I want to introduce you hypocycloid and epicycloids. A hypocycloid is a curve traced out by a fixed point P on a circle C of radius b as C rolls on the inside of a circle with center O and radius a. Its parametric equation is If the circle C rolls on the outside of the fixed circle, the curve traced out by P is called an epicycloid (see fig. 3). Then its parametric equation is

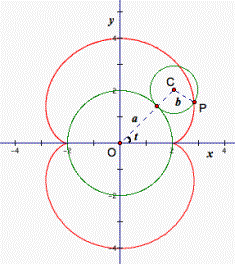
Figure 3

Maybe some of you would say that cycloid seems so simple and common but why it is called as “Helen of Geometry”. That is because is related to one of the most famous pairs of problems in the history of calculus. The first problem, called tautochrone problem, began with Galileo and completed by Christian Huygens. The tautochrone problem is that the time required to complete a full swing of a given pendulum is approximately the same whether it makes a large movement at high speeds or a small movement at lower speeds. The second problem, called brachistochrone problem, is to determine the path down which a particle will slide from point A to point B in the shortest time. This problem was proposed by John Bernoulli in 1696 as a challenge to the mathematicians of Europe. Newton, Leibniz, I’Hopital, and John and James Baernoulli all found the correct solution. Just because the two problems attracted so many great mathematicians and physicists, cycloid is called as the “Helen of Geometry”.