Explore Conics Family

Najia Bao

When technological tools are available, students can focus on decision making, reflection, reasoning, and problem solving (NCTM 2000).

Now we use Graph Calculator to explore problem 3 in the 11^th assignment.

Problem 3

Investigate with different values of d

for e > 1, e = 1, e < 1.

Now let’s recall the concepts and theorems related to polar equations of conics.

1. The locus of a point in the plane whose distance from a fixed point (focus) has a constant ratio to its distance form a fixed line (directrix) is a conic. The constant ratio e is the eccentricity of the conic.

2. A polar equation of the form or represents a conic section with eccentricity e. The conic is an ellipse if e < 1, a parabola if e =1, or a hyperbola if e > 1. And ôdô is the distance between the focus at the pole and its corresponding directrix.

Next let’s begin our graphical reasoning.

What happens?

When we investigate with different positive values of d

Now let’s use Graph Calculator to graph the polar equations.

For e = 1, when d = 1, 2, 3, and 4 respectively, the graphs of four types of equations shown in Figure 1, 2, 3, and 4 can be classified as follows:

Vertical directrix left the pole: (see fig. 1).

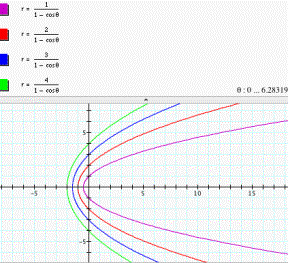
Figure 1

Vertical directrix right the pole: (see fig. 2)

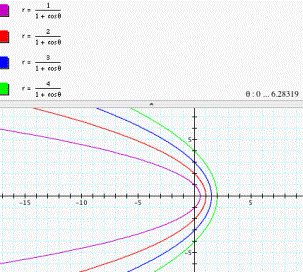
Figure 2

Horizontal directrix below the pole: 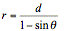(see fig. 3)

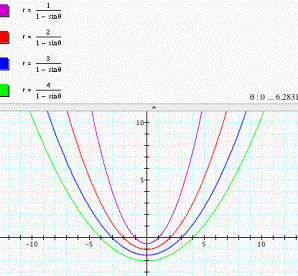
Figure 3

Horizontal directrix above the pole: 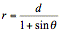(see fig. 4)

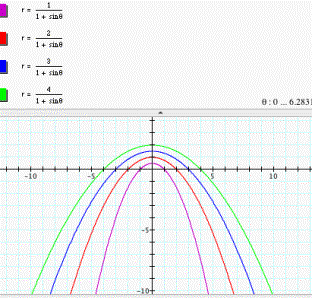
Figure 4

Until now we can see how the shape of parabola changes as the value of d changes.

For e < 1, suppose e = 0.7, and when d = 1, 2, 3, and 4 respectively, the graphs of four types of equations shown in Figure 1, 2, 3, and 4 can be classified as follows:

Vertical directrix left the pole: (see fig. 5).

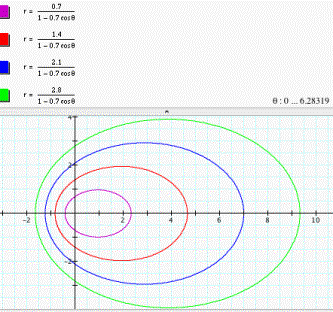
Figure 5

Vertical directrix right the pole: (see fig. 6)

Figure 6

Horizontal directrix below the pole: 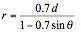(see fig. 7)

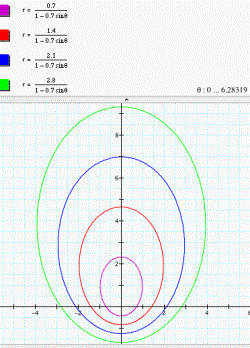
Figure 7

Horizontal directrix above the pole: 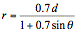(see fig. 8)

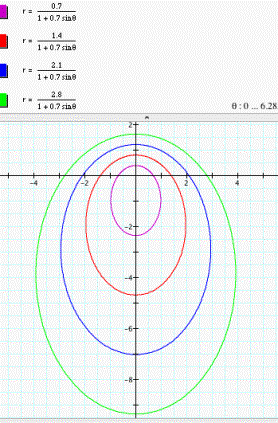
Figure 8

Until now we can see how the shape of ellipse changes as the value of d changes.

For e > 1, suppose e = 1.5, and when d = 1, 2, 3, and 4 respectively, the graphs of four types of equations shown in Figure 1, 2, 3, and 4 can be classified as follows:

Vertical directrix left the pole: (see fig. 9).

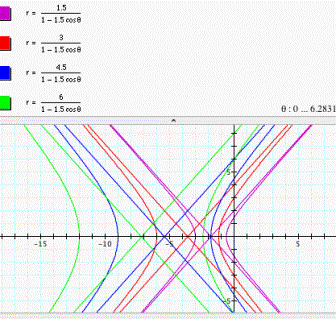
Figure 9

Vertical directrix right the pole: (see fig. 10)

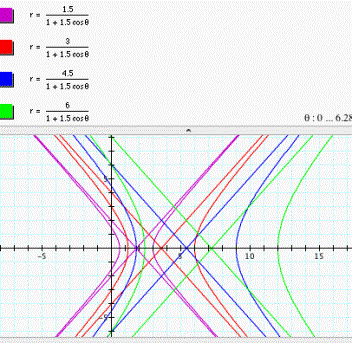
Figure 10

Horizontal directrix below the pole: 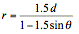(see fig. 11)

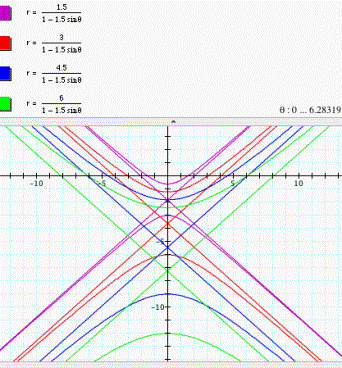
Figure 11

Horizontal directrix above the pole: 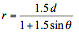(see fig. 12)

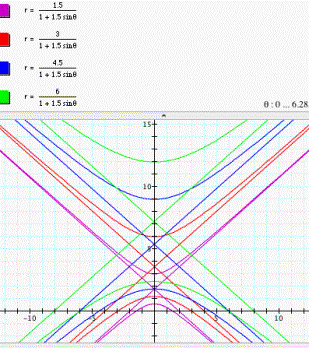
Figure 12

Until now we can see how the shape of hyperbola changes as the value of d changes.

One Interesting and amazing phenomenon:

Two groups of curves are coincident

When we go on to investigate with different negative values of d, we find an interesting and amazing phenomenon that the group of the curves and the group of the curves are coincident (see fig. 13 & fig. 14). That is because any point (-r, q) on the curve represents the same point as any point (r, q + p) on the curve .

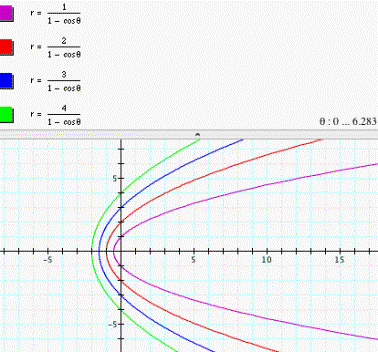
Figure 13

Figure 14

Another Interesting and amazing phenomenon:

Two groups of curves are orthogonal

When we continue our exploration, we find another interesting and amazing phenomenon, that is, two groups of curves and are orthogonal (see fig. 15). As we know, an orthogonal trajectory of a group of curves is a curve that intersects each curve of the group orthogonally, that is, at right angles. We say that the two groups are orthogonal trajectories of each other. This is really a strange phenomenon. But it can be explained by differential equations. The first step of the proof is to write a differential equation that is satisfied by all members of the group. This means to find the slope of the tangent line at any point on one of the group of curves. The second step is to solve the differential equation. Due to the time limitation, the detail of proof we will discuss next class. So much for today.

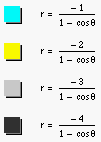
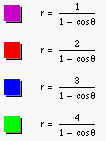
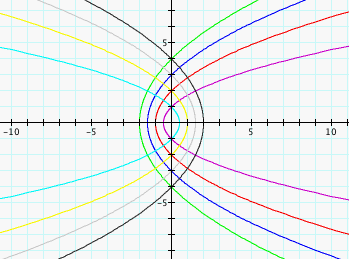
Figure 15