
The
Spreadsheet and Linear Regression Equation
Najia
Bao
Good morning. Today we will explore linear
regression equation by Excel.
As we know, a linear function which can be described
by an equation of the form y = ax + b, where a and b are constants. Recall that
the graph of every function of this form is a line with slope a and y-intercept
b. Now letŐs solve problem 8 in this assignment.
Problem
8
Use the Cooled Data to explore
and generate a function to predict.
Suppose that we take a cup of hot water and measure its
initial temperature which is 212 ˇF (time = 0) and then record
temperature readings each minute for 30 minutes (see table 1). And it is
assumed that the room temperature is 75ˇF.
Table 1. The Cooled Data
|
Time (minutes) |
Temperature (ˇF) |
Time (minutes) |
Temperature (ˇF) |
|
0 |
212 |
16 |
152 |
|
1 |
205 |
17 |
150 |
|
2 |
201 |
18 |
149 |
|
3 |
193 |
19 |
147 |
|
4 |
189 |
20 |
145 |
|
5 |
184 |
21 |
143 |
|
6 |
181 |
22 |
141 |
|
7 |
178 |
23 |
140 |
|
8 |
172 |
24 |
139 |
|
9 |
170 |
25 |
137 |
|
10 |
167 |
26 |
135 |
|
11 |
163 |
27 |
133 |
|
12 |
161 |
28 |
132 |
|
13 |
159 |
29 |
131 |
|
14 |
155 |
30 |
130 |
|
15 |
153 |
|
|
We use the following chart (see fig. 1) to demonstrate the
data in table 1.
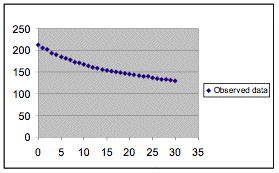
Figure 1
As we know, a straight line called the linear regression
line can model many data sets. Excel provides the slope and intercept functions
to calculate the slope and y intercept of the linear regression line for a set
of data pairs. LetŐs have a look at a linear model –the purple line
constructed by Excel. We can see there are two sets of points – the
scattered ones are the actual data (black) while the straight line (purple) is
the linear – regression line (see fig. 2).
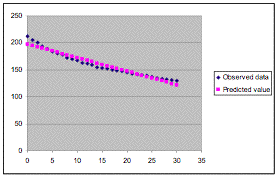
Figure 2
When we know the slope and Y
intercept of a linear regression line, we can calculate predicted values of y
for any x using the formula y = ax + b. Now letŐs use the function y = -2.52x +
197.32 predict the temperature at 45th minute, which is 84.12ˇF (see fig. 3).
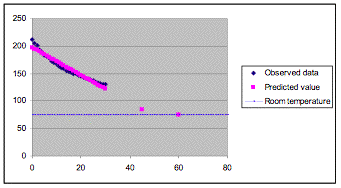
Figure 3
We should notice that at the 60th
minute, the temperature is 75ˇF (see fig 3.) but not the result of
computation which is 46.37ˇF based on the function because the
temperature decreased to the room temperature 75ˇF at the 49th minute.
Similarly the temperature is still 75ˇF at the 300th minute
(see fig 4.).
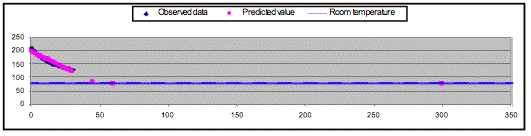
Figure 4
Conclusion
This is why whenever we write and solve word
problems, we should always take into account situations in the real world.