Explore Quadratic Equation and Its Roots

By Graphing Calculator

Najia Bao

When technological tools are available, students can focus on decision making, reflection, reasoning, and problem solving (NCTM, 2000).

This lesson is an excellent opportunity for using technology to explore quadratic equations and roots.

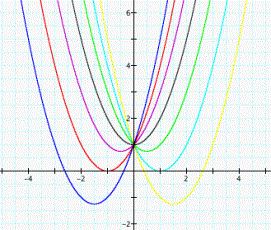
Investigation 1-3

For the general quadratic equation y = ax² + bx + c, if we set a = 1 and c =1, that is to say, y = x² + bx + 1, and then we set b = -3, -2, -1, 0, 1, 2, 3, we can see the “movement” of a parabola as b is changed (see fig. 1).

In figure 1, the blue curve represents the parabola with b = 3, the red one represents the parabola with b = 2, the purple represents the parabola with b = 1, the black represents the parabola with b = 0. And the green, light blue, and yellow represents the parabola with b = -1, -2, -3 respectively. It seems that when b is negative, the parabola “moves” to the right and when b is positive, it “moves” to the left. We also noticed that when b = 3, the equation has two negative real roots. That is because the parabola intersects the x-axis at two points. Similarly, when b = - 3, the equation has two positive real roots. When b = 2 or –2, the parabola is tangent to the x-axis, so the equation has just one real root, which is -1 or 1 respectively. When –2 < b < 2, the equation has no real roots because the parabola does not intersect the x-axis.

From figure 1, we also found something else interesting. All of the parabolas passes through the point (0,1). That is because whenever x =0, y = x² + bx + 1 = 0 + 0 +1 =1.

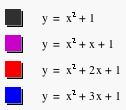
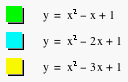
Figure 1

Furthermore, we found an amazing and interesting phenomenon that the locus of the vertices of the set of parabolas graphed from y = x² + bx + 1 is the parabola y = -x² + 1 (see the red parabola in fig. 2).

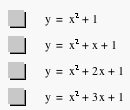
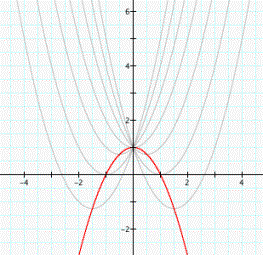
Figure 2

Now let’s substitute y for b. So x² + bx + 1 = 0 is changed to x² + yx + 1 = 0. Then we get the following graph (see fig. 3).

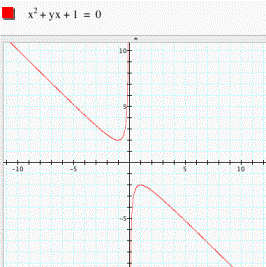
Figure 3

Then we add another equation y = 3, which is a line paralleling to x-axis (see fig. 4). We find that the line y =3 intersects the original curve at two points. Therefore, the system of equations x² + yx + 1 = 0 and y = 3 has two negative real roots. From figure 4, we also find that the system of equations has always two real roots as long as y > 2 or y < -2, and the system of equations has just a distinct real root when y = 2 or –2. Of course, we can also imagine that when -2 < y < 2, it has no real root.

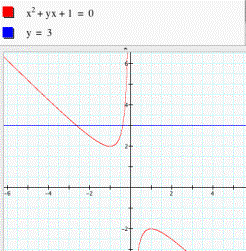
Figure 4

Next, let’s change the value of c from 1 to –1, that is, the original equation is changed to x² + yx - 1 = 0 (see fig. 5). And then we add a new linear equation 2x + y = 0, that is, y = -2x (see fig. 5). From figure 5, we find that it intersects the curves representing the quadratic equation x² + yx + 1 = 0 at two points, thus the system of equations comprised of them has two real roots (one positive and the other negative). Also, we find that the line 2x + y =0 does not intersect the curves representing the quadratic equation x² + yx - 1 = 0, thus there is no real roots.

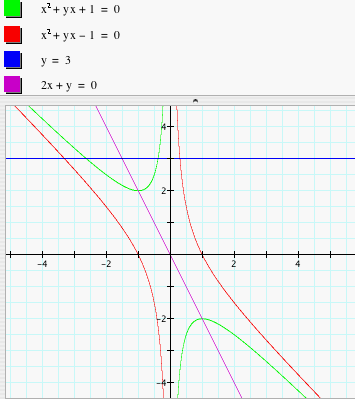
Figure 5