How to Prove Concurrence of Three Lines

and Collinear of Three Points

Najia Bao

Proof is the heart of mathematics as individuals explore, make conjectures, and try to convince themselves and others about the truth or falsity of their conjecture. Proof of concurrence of three lines and collinear of three points is a typical topic of geometric proof in secondary school. Yet students often find such kind of proof difficult. For instance, prove that the lines of the three altitudes of a triangle are concurrent. Another example, prove that the feet of the perpendiculars from an arbitrary point on the circumcircle of a triangle to the sides of the triangle are collinear (Simson line). How to prove concurrence of three lines and collinear of three points? There are many methods. Here, I just introduce two main and convenient thinking ways which are 180° strategy and stretch strategy.

Teaching these thinking way also provides a good opportunity for students to “produce logical arguments and present formal proofs that effectively explain their reasoning” (NCTM 2000) as they learn and apply multiple thinking ways of proof with certain difficulty level.

Now I give you the proof of problem 13 in this assignment.

Problem 13

Prove that the lines of the three altitudes of a triangle are concurrent (see fig. 1).

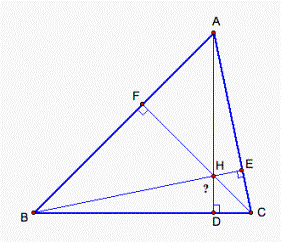
Figure 1.

Proof by stretch strategy

Let H be the intersection of the two altitudes BE and AD of the triangle ABC. Construction: Connect the points C and H and extend the segment CH to intersection with AB at point F.

Step 1. Because mAEB = mADB = 90°, AEDB are four-points-on-one-circle. So ABE = ADE. Also, since mBEC = mADC = 90°, HECD are four-points-on-one-circle. So HCE = HDE. Then we get that ABE = HDE.

Step 2. Since ABE = FCA and BAE = CAF, so D BEA and D CFA are similar. Then we get that mCFA = mBEA = 90°. Thus CF is also an altitude of triangle ABE and AD, BE, and CF interest at the point H (see fig. 2).

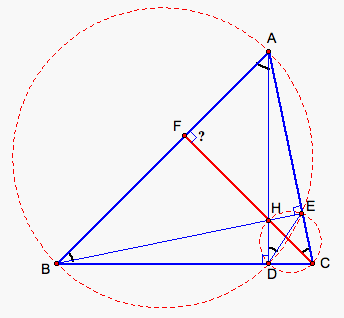
Figure 2.

Proof by180° strategy

Step 1. Let H be the intersection of the two altitudes BE and AD of the triangle ABC. Auxiliary construction: Connect the points C and H. Let HF ^ AB. Now we need to prove that mFHC = 180° (see fig. 3).

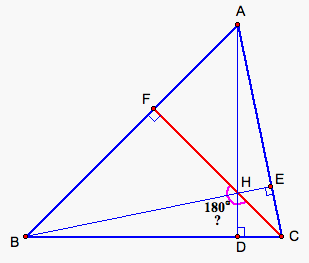
Figure 3.

Step 2. Since mADB = mAEB = 90°, AEDB are four-points-on-one-circle. So EDC = BAE. Since mAFH = mAEH = 90°, AFHE are four-points-on-one-circle. So FHB = FAE. Since mBEC = mADC = 90°, HECD are four-points-on-one-circle. So EDC = EHC. Then we get that EHC = EDC = FAE = FHB.

Step 3. Because mEHC + mCHB = 180°, then we get mFHB + mBHC = 180°. Thus C, H, and F lie on the same line and CF is an altitude of the triangle ABC (see fig. 4).

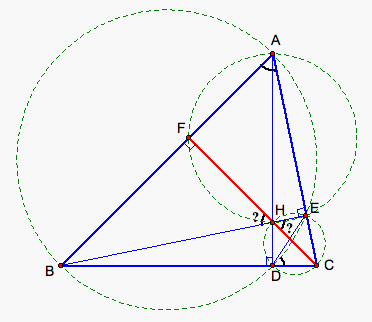
Figure 4

We have already proved the concurrence of three lines by using 180° strategy and stretch strategy. Next we will explore the application of two strategies to prove collinear of three points, which is also a problem making students headache.

Proof about Simson line:

Prove that the feet of the perpendiculars from an arbitrary point on the circumcircle of a triangle to the sides of the triangle are collinear (see fig. 5).

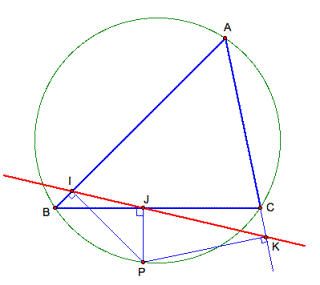
Figure 5

Proof by180° strategy (see fig. 6)

Step 1. Since mBIP = mBJP = 90°, IJPB are four-points-on-one-circle. So IJB = IPB. Also, since mPJC = mCKP = 90°, JCKP are four-points-on-one-circle. So CJK = CPK.

Step 2. Since ABPC are four-points-on-one-circle. So KCP = ABP.

Step 3. Since mKCP + mCPK = 90°, then mKCP + mCJK = 90°. Similarly, mABP + mIPB = 90°, then we get mABP + mIJB = 90°. Thus KCP + CJK = ABP + IJB, then we get CJK = IJB.

Step 4. Since mBJK + mKJC = 180°, mIJB + mBJK = 180°. Thus the points I, J, and K are collinear.

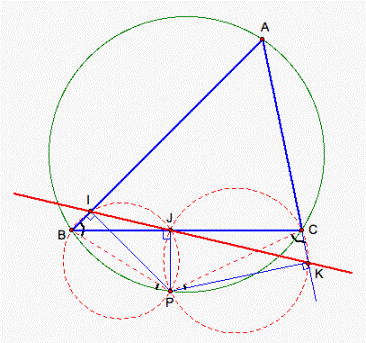
Figure 6

Due to the space limitation, here, we just demonstrate the proof by 180° strategy. We suggest you to try to prove Simson line theorem by stretch strategy.