The Use of ÒEquilateral TriangleÓ Strategy in Proof:

Fermat Point, 100 degree Isosceles Triangle, etc.  

 

Najia Bao

 

 

            Good morning, I like to teach math strategy, so today I want to introduce Òequilateral triangleÓ strategy. It is a useful tool for us to solve some difficult geometric problems such as the proof about Fermat point, Jim WilsonÕs 100 degree Isosceles Triangle, and some problems of International Mathematical Olympiad Competition. ÒEquilateral triangleÓ strategy refers to adding one or more auxiliary line to construct one or more equilateral triangles in order to prove or solve geometric problems. Since in any equilateral triangle, three angles are equal to 60¡ and three sides are equal, which contribute to solve problems. Thus, this strategy, just as a double-edged sword (reversible), helps us quickly cut a path which is overgrown with mathematical brambles.

 

 

Problem 1 (Problem 11 in assignment 6)

 

       Consider any triangle ABC. Find a construction for a point P such that the sum of the distances from P to each of the three vertices is a minimum.

 

       LetÕs use GSP to demonstrate the problem. Look, we find something interesting. It is a pattern that in any triangle, when mAPB - mBPC =mCPA=120¡,  the sum of the distances from P to each of the three vertices is a minimum (see fig. 1). 

 

 

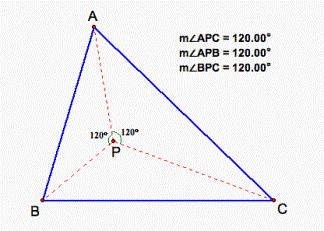
Figure 1.

 

 

To explore the pattern, we use Òequilateral triangleÓ strategy and do auxiliary construction: three equilateral triangles ABF, AEC, and BCD, and connect the points A and D, B and E, C and F (see fig. 2). LetÕs go on. Wow! The GSP tell us another strange thing: the three line segments AD, BC, and CF intersect in a point, and what is more amazing, this point and the point P coincide with each other. Also we find AP+BP+PC = AD = BE = CF.   

 

 

 

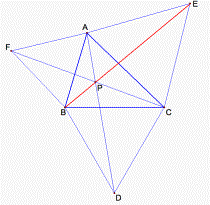
Figure 2.

 

 

Now letÕs start formal auxiliary construction: we draw three equilateral triangles DABF, DBCD, and DACE. Connect the points B and E, C and F. BE and CF intersect in a point P, and we also connect the points A and P. According to the construction, AB=AF, AE=AC, and FAC=BAE, so DAFC and DABE are congruent. Thus we get ABE=AFC (see fig. 3)。

 

 

 

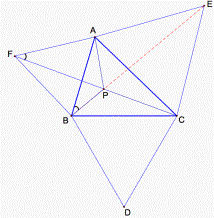
Figure 3.

 

 

          In order to prove that the sum of the lengths of AP, BP, and CP is a minimum, we need two steps:

          Firstly, letÕs prove AP+BP+CP=BE.

          We find a point G on the segment BE and let PG=AP. Connect the points A and G. As we know, DAPG is an equilateral triangle, thus AG=PG. Furthermore, since mAGE=mAPC=120¡, AE=AC, and AP=AG, we get the result that DAGE and DAPC are congruent. Therefore, AP+BP+PC=BE (see fig. 4).

 

 

 

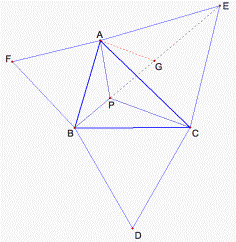
Figure 4.

 

 

          Secondly, we need to prove the sum of the lengths of AP, BP, and PC is a minimum.

          Let M be an arbitrary point but not the point P in DABC, and connect the points A and M, B and M, M and C. Now letÕs try to prove the sum of the lengths of AM, BM, and MC is greater than the sum of the length of AP, BP, and CP, that is, AM+BM+MC > AP+BP+PC.

         Similarly, we can prove that AM+BM+MC＝BM+MN+NE. Because BMNE is a broken line, AM+BM+MC＝BM+MN+NE > BE= AP+BP+PC (see fig. 5).

 

 

 

 

 

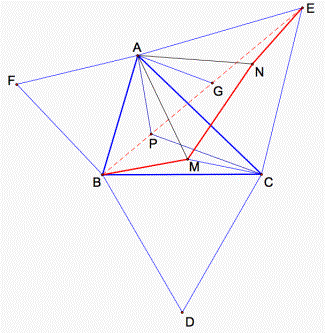
Figure 5.

 

 

 

 

Problem 2: 100 degree Isosceles Triangle (Item from Jim WilsonÕs web site EMAT 6600)

 

Given an isosceles triangle ABC with AB = AC and the measure of angle BAC = 100 degrees. Extend AB to point D such that AD = BC. Now draw segment CD. What is the size of angle BCD? 

 

 

 

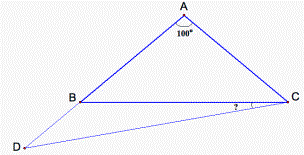
Figure 6.

 

 

           Why we use Òequilateral triangleÓ strategy to solve this problem? Because it is an isosceles triangle, and the measurement of its top angle BAC is 100¡, which means the two base angles are 40¡. Then we get 100¡ －40¡ ＝ 60¡, which rings a bell and remind us to use Òequilateral triangleÓ strategy.

Solution: Auxiliary construction: Equilateral triangle ADE (see fig. 7). According to the construction, AD = DE = AE, and mDAE = 60¡, mCAE = mBAC - mDAE = 100¡ - 60¡= 40¡. Since ABC = CAE, AB = AC, and BC = AE, DBAC and DACE are congruent. Therefore mACE = m BAC = 100¡. Since AD = ED, AC = EC, and DC = DC, DDAC and DDEC are congruent. Therefore mACD = mECD = ½ « 100¡ = 50¡, and mBCD = mACD - mACB = 50¡ - 40¡ = 10¡ (fig.7).

 

 

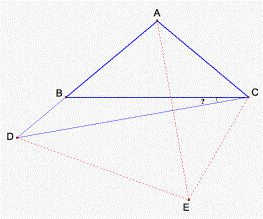
Figure 7.

 

 

Problem 3:

Let ABC be an isosceles triangle (AB=AC). Angle BAC equals 20 degrees. Point P belongs to AB, and the distance AP is equal to BC. Find the measure of angle ACP.  

 

 

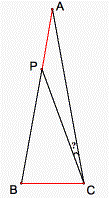
Figure 8.

 

       Again, why we use Òequilateral triangleÓ strategy to solve this problem? Because it is an isosceles triangle, and the measurement of its top angle BAC is 20¡, which means the two base angles are 80¡. Then we get 80¡ －20¡ ＝ 60¡, which also rings a bell and remind us to use Òequilateral triangleÓ strategy.                                                          

 

 

Hint: (see fig. 9).

 

 

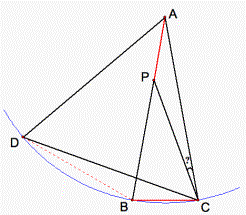
Figure 9.

 

 

          Next, IÕll give you two more examples. We can also quickly solve them by  Òequilateral triangleÓ strategy. Of the followings two items, Problem 4 is from 43rd International Mathematical Olympiad Competition (2002) and Problem 5 from 38th International Mathematical Olympiad Competition (1995).

 

Problem 4:

       BC is a diameter of a circle center O. A is any point on the circle with angle AOC > 60o. EF is the chord which is the perpendicular bisector of AO. D is the midpoint of the minor arc AB. The line through O parallel to AD meets AC at J. Show that J is the incenter of triangle CEF.

      (Item from 43rd International Mathematical Olympiad Competition, 2002)

 

 

 

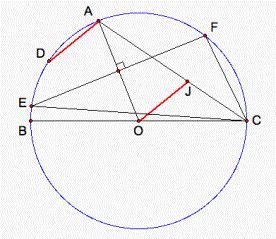
Figure 10.

 

 

Hint: (see fig. 11).

 

 

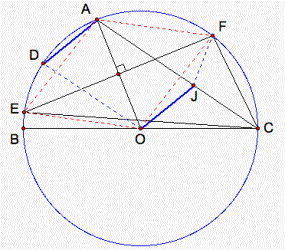
Figure 11.

 

 

 

Problem 5.

        Let ABCDEF be a convex hexagon with AB = BC = CD and DE = EF = FA such that mBCD = mEFA = 60¡. Suppose that G and H are points in the interior of the hexagon such that mAGB = mDHE = 120¡. Prove that AG + GB + GH + DH + HE CF.

        (Item from 38th International Mathematical Olympiad Competition, 1995)

 

                                                                                                              

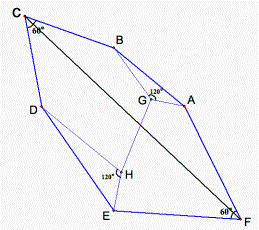
Figure 12.

 

 

Hint: (see fig. 13).

 

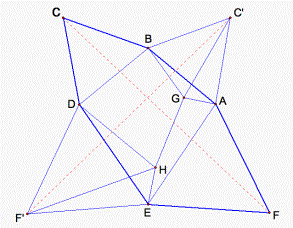
Figure 13.