Intersecting Loci Principle In Geometric Construction

Najia Bao

I like to use the Geometer’s Sketchpad, because it is a very helpful tool. It allows us to investigate, demonstrate, and explore, specially to find geometric loci.

As we know, the solution of a geometric construction problem depends upon the finding of a point, which satisfies certain conditions. In order to locate the point, we need two conditions, that is to say, we can try to locate the point by finding the intersecting point of two loci (lines or circles). We usually call the method “intersecting loci”. If we know lots of geometric loci, we can discover immediately where the required point is to be located. But it is not easy to solve construction problem. Of course, it is easy to find one locus, but what makes the problems difficult is that we need to find another locus. GSP, as a means, helps us to visualize and demonstrate.

Now we begin with the following problem.

Problem 14. Given a line and a circle with center O. Take an arbitrary point P on the circle. Construct two circles tangent to the given circle at P and tangent to the line.

This is a difficult construction problem. Consider the given problem. The center of the desired circle will lie along a line from the center O of the given circle with the specified point P (see fig. 1).

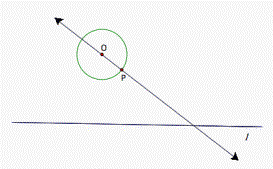
Figure 1.

But this is just the first locus, which is easy to find. We have to find the second locus to make O’P = O’B, and O’B be perpendicular to the line l (see fig. 2).

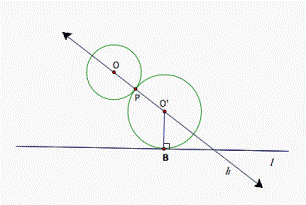
Figure 2.

Now we try to look for the other locus for the center O’ of the tangent circle, which is difficult to find. Suppose the problem had been solved, we would have the following figure (see fig. 3):

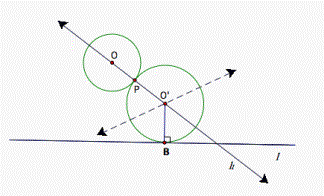
Figure 3.

How to find the second locus? As we know, the locus of a point equidistant from two intersecting lines consists of the two bisectors of the angles formed by the two given lines. We also know O’ should be the point of intersection of the two loci. Finally, a bisector of PAB formed by the two lines l and l₂. l₂ is tangent to the given circle at the point P (see fig. 4).

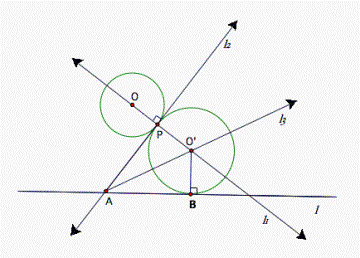
Figure 4.

There are two solutions for this construction problem, because not only PAB but also PAB’ are angles formed by the two lines l and l_2. So we find the other circle whose center O” is the point of intersection of the loci - line l₁nd l₄The following is the other solution (see fig. 5):

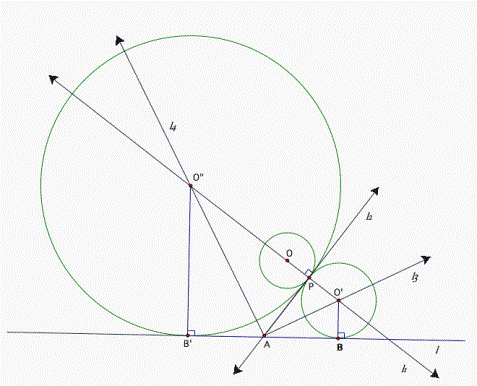
Figure 5.

The above are my analysis and construction. Now I want to give a proof and discussion on the construction problem.

Proof. Since O’ lies on the bisector of PAB, O’P ^ l₂, and O’B ^ l, so O’B = O’P which are equal to the radius of the required circle. Therefore, the circle with the center O’ is just the required circle.

Similarly, we can prove that the circle with the center O” is also the required circle.

Discussion. From the proof above, we conclude that generally there are two solutions for this geometric construction problem. But there are two situations that there is only one solution, when the given point P lies on a line which is perpendicular to the line l and through the center O of the given circle. The following figures are the two cases (see fig. 6 & fig. 7).

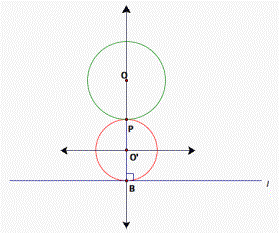
Figure 6.

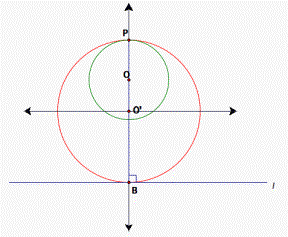
Figure 7.

Whenever we do geometric construction, we should keep in mind the most important and most frequently useful geometric loci, such as the locus of a point equidistant from two given points which is the perpendicular bisector of the given segment, and the locus of a point equidistant from two intersecting lines indefinitely produced which consists of the two bisectors of the angles formed by the two given lines. But, for problems with difficult level, it is not enough to only depend on knowledge of such geometric loci. We also need to apply a variety of problem solving strategies and methods, such as dilation and tail construction. Apollonius’ problems, PLL and PCC, the classical problems in geometric construction (see Jim Wilson’s Web site), can be solved by combining general geometric loci with dilation (see fig. 8 & fig. 9).

PLL: Draw a circle passing through a given point and tangent to two given lines.

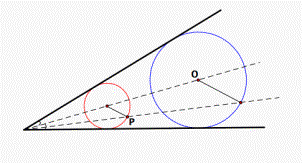
Figure 8.

PCC: Draw a circle passing through a given point and tangent to two given circles.

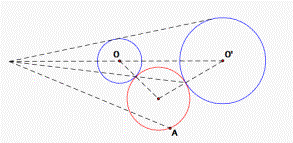
Figure 9