Area Strategy

Najia Bao

Good morning. Today I want to talk about “area” strategy, which is quite useful for us to solve some problems with middle level of difficulty. Area strategy refers to a method of proof, that is, using area formula to prove the relationship of geometric quantities based on the relationship between the areas of different geometric figures.

Now with GSP software, I use area strategy to prove problem 11 in this assignment.

Problem 11

Construct any acute triangle ABC and its circumcircle. Construct the three altitudes AD, BE, and CF. Extend each altitude to its intersection with the circumcircle at corresponding points P, Q, and R (see fig. 1).

Figure 1.

It is difficult to solve this problem. So we need to explore by using GSP. As we change the triangle ABC shape with its circumcircle, which leads to the change of the lengths of AP, AD, BQ, BE, CR, and CF, we find that the sum of is a constant, which is 4.

Now the focus of our study is how to prove the result that = 4. Firstly, we can view AP as the sum of AH + HD + DP, or the sum of AD + DP. If we view AP as the sum of AD + DP, then we get

Therefore,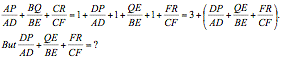

It is very difficult to get the answer.

Fortunately, again, GSP helps us to find the result: DP = HD, QE = HE, and FR = FH (see fig. 2).

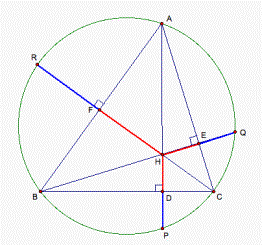
Figure 2.

By using area strategy, we can quickly get the result: HD/AD + HE/BE + HF/CF =1. The procedure of the proof is as followings:

Firstly, we prove that DP = HD. QE = HE, and FR = FH.

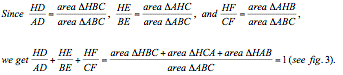
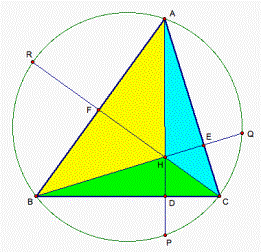
Figure 3.

Construct auxiliary lines: connect the points P and C. If D HDC and DPDC are congruent, then we can get the result that HD = PD. How to prove that D HDC and DPDC are congruent? We notice that both of them are right triangles because the point D is the foot of the altitude AD. Since CF ^ AB and AD ^ BC, the four points F, H, D, and B are on the same circle. Hence CHD = FBD. And since APC = ABC, we get CHD = CPD. So D HDC and DPDC are congruent (see fig. 4).

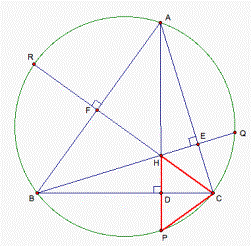
Figure 4.

Therefore, we get HD = PD. Similarly, we get QE = HE, and FR = FH.

Finally,

However, with area strategy, it is much easier to get the answer.

Now I prove Ceva’s Theorem by area strategy.

Problem 2. (item from Jim Wilson’s Web site)

Ceva’s Theorem: The lines joining the vertices of a given triangle to a given point determine on the sides of the triangle six segments such that the product of three of these segments having no common end is equal to the product of the remaining three segments.

Suppose AO, BO, and CO intersect BC, CA, and AB at D, E, F respectively in an arbitrary triangle ABC (see fig. 5), prove that

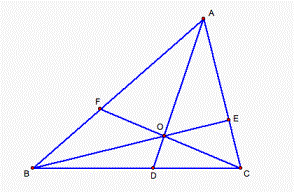
Figure 5.

Now we begin our proof.

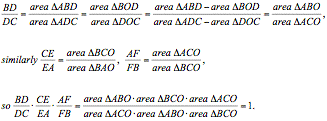
In fact, lots of problems can be solved by area strategy. I give you five more problems as followings:

1. In DABC, AB < AC. BD and CE are two altitudes of DABC. Prove that:

CE > BD.

2. To prove: The sum of the distances from any point on the base of an isosceles triangle to the legs of the triangle is the altitude of the side of the isosceles.

3. Given the lengths of the two legs of a right triangle ABC, find the length of the radius of its inscribed circle.

4. Let O be any point on the median of the line segment AM in DABC. BO intersects AC at point D, CO intersects AB at point E. Prove that DE // CB.

5. In DABC, AB = 15, AC = 20, AD is perpendicular to BC at point D, AD = 12, and AE is the bisector of the angle BAC. Find the length of AE.