When Is a Geometric Problem Worth One Hundred Geometric Problems?

Najia Bao

Problem solving is an important component of learning mathematics, and that topic continues to receive significant attention in recommendations for school mathematics (NCTM 2000). We should give students much more opportunities to solve geometric problems with difficult level. Through dealing with a synthetic and difficult problem, students may review lots of knowledge and methods. The fourteenth problem in the ninth assignment (see Jim Wilson’s EMAT 6680) is such a typical sample. To solve this problem, we need to apply many theorems regarding midsegment of triangles, isosceles trapezoid, congruent triangles, angle relationships in circles, four-points-on-a-circle, and so on. The problem is very helpful for us to develop the divergence, broadness, and flexibility of our students’ thinking.

Problem 14.

Construct the Simson line of a point P (on the circumcircle) and construct the segment connecting P to the Orthocentner. How do the two segments intersect?

It is very difficult to solve this problem about Simson line. So we need to explore by using GSP. As we move the point P along the circumcircle of the triangle ABC, we notice that the segment HP is always bisected by the Simson line IJK, that is to say, PX = XH (see fig. 1).

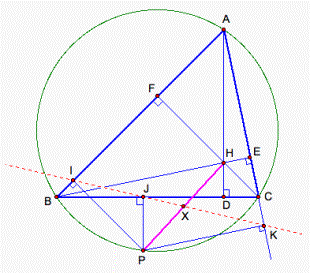
Figure 1.

Now let’s analyze this difficult problem first. In order to prove PX = XH, passing through point H, we draw a line parallel to segment line IK to construct a triangle PHM. If MJ = JP, then we get PX = XH (the converse of Midsegment theorem). But to prove MJ = JP, we must prove quadrilateral HMPQ is an isosceles trapezoid, and then we need to prove HD = DQ (see fig. 2).

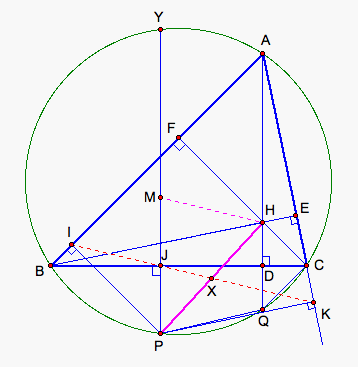
Figure 2.

Next we’ll start to our proof of this problem. First, prove HD = DQ. Second, prove that HMPQ is an isosceles trapezoid. Third, prove MH//IK.

First, prove HD = DQ. Construct auxiliary lines: connect the points Q and C. If D HDC and D QDC are congruent, then we can get the result that HD = QD. How to prove that D HDC and DQDC are congruent? We notice that both of them are right triangles because the point D is the foot of the altitude AD. Since CF ^ AB and AD ^ BC, the four points F, H, D, and B are on the same circle. Hence CHD = FBD. And since AQC =ABC, we get CHD = CQD. So D HDC and DQDC are congruent. Therefore, we get HD = QD (see fig. 3).

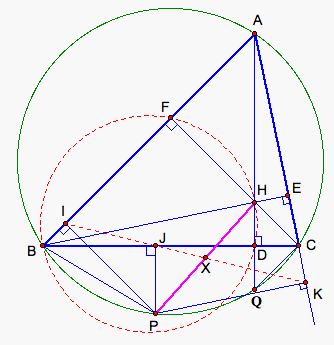
Figure 3.

Second, prove that HMPQ is an isosceles trapezoid. Extend segment PJ to its intersection with the circumcircle of DABC at point Y. Since YP ^ BC, AQ ^ BC, so YP//AQ. Now we get that the quadrilateral AYPQ is an isosceles trapezoid, and AY = QP. Passing through point H, let HM be parallel to AY, and we get HM = AY. So HM = QP and HMPQ is an isosceles trapezoid. Since JD perpendicularly bisects HQ, JD also perpendicularly bisects MP, that is, MJ = JP (see fig. 4).

Third, prove MH//IK. Given mBIP = mBJP = 90°, then the four points I, B, P, and J lie on a circle with BP as its diameter. So we get that YJI = IBP. And since AYP = ABP, we get that AYP = YJI and AY // IK. Furthermore, we get that MH // IK. Since MJ = JP, then we get that the segment PH is bisected by IK (see fig. 4).

Figure 4.

To solve the above difficult problem, we use “auxiliary circle” strategy which is a very important geometric strategy. By constructing one or more auxiliary circles, we apply the properties of circle to solve geometric problems. This strategy is often used in finding the measurement of angles and length of segments, proving equality about angles and segments, and complicated relationship between segments. It is very useful to solve considerably difficult problems.