The idea of a center of a circle is fairly straightfoward. It is that single point such that all the points on the circle are an equal distance away from that point and that distance is the length of the radius. The center is also a place on a solid circle, such as a plate or a pizza crust, where it can be balanced. This is what allows people to do plate spinning on poles. The center of a triangle is less well defined. The center could be the point that is the same distance, or equidistant, from all three vertices. Another option is that the point is equidistant from all three sides. The center could be defined as the center of gravity, which is the point on which it could balance on an object such as a pin. It might surprise the student to know that these described notions of center are only a few of the options for a triangle and in the vast majority of triangles they represent distinct points! During this assignment we will be focusing on the third notion of center as well as some other interesting and important properties about triangles.

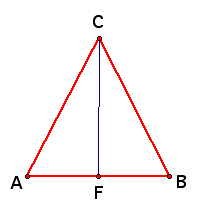
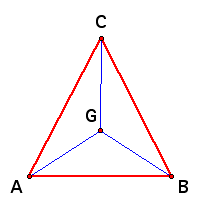
In order to construct the center of gravity on a triangle we need to create the medians of the triangle. The median of a triangle is a line segment that goes from a vertex to the midpoint of the opposite side.

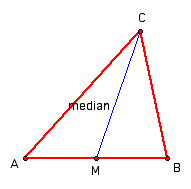
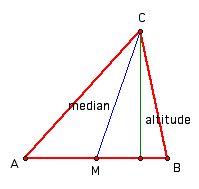
A very important characteristic of the median is that it cuts the triangle into two smaller triangles that have equal areas. To see this remember that the area of a triangle is 1/2*base*height. Since the median is defined as going from a vertex to the midpoint of the opposite side then it should be clear that the bases of the newly formed triangles are equal. The heights are also equal because the height is defined a being the length of the altitude, the line segment extending from the vertex to its opposite side, the base, at a ninety degree angle. Since there is only one altitude from vertex C, the triangles AMC and BMC share an altitude and consequently have the same height. Therefore, since AMC and BMC have the same height and equal bases lengths they have equal areas. Also take note that since the sum of the areas of the smaller triangles equals the area of the large triangle, area(AMC)+area(BMC)=area(ABC), and since the area of the smaller triangles equal each other, area(AMC)=area(BMC), then the area of the large triangle is twice the area of each of the small triangles, 2*area(AMC)=area(ABC)=2*area(BMC).

Now that we know what a median is, construct all three medians on a triangle and find their interesection point. This point is called the centroid, denoted G, and is the center of gravity for this triangle.

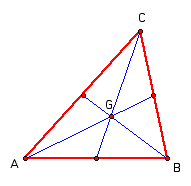
There are several important facts about this constructed triangle that should be noted. The first is that the six smaller triangles formed all have equals areas. Next is the claim that all three medians are concurrent, meaning they intersect at a single point. Although it seems clear in the picture, the concurrency of three segments is no trivial thing and needs to be proved. The last characteristic that needs to be discussed is how the centroid cuts each median in such a way that distance from the centroid to the vertex is twice as long a the distance from the centroid to the midpoint. Once we are done exploring these ideas you will have a better understanding of an important concepts related to the subject of triangles.

First, we will show that when all three medians are drawn the triangle is broken up into six triangles of equal area. Please, don't just take my word for it. Click here to convince yourself. Grab any of the three green vertices A, B or C and drag it across your screen. At the top of the page the areas of all six of the small triangles is being measured interactively along with the area of the large triangle and the value of one-sixth the area of that large triangle. Notice that that area of all six of the small trianlges equals one-sixth the area of the large triangle, no matter what the large triangle looks like.

Remember that each median cuts the original triangle into two triangles of equal area. Begin by drawing each of the medians on seperate triangles so that you can see the different triangles that have matching areas. Since each small triangle has an area that is half the area of the large triangle, all the of the small triangles in the picture have the same area.

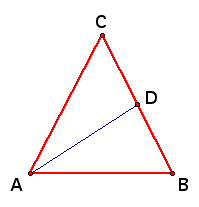
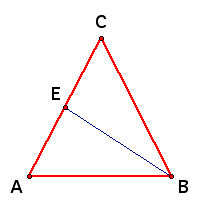
Now draw a single triangle with all three medians.

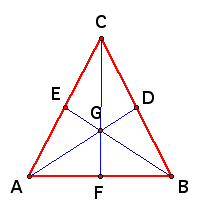
All we need to do this proof is to remember that a median splits any triangle into two triangles of equal length. Looking at the medians of the large triangle ABC we know that

This is seen clearly with the images of the three medians drawn in seperate triangles. Now observe the triangle in which all three medians are drawn on one triangle. The line segments going from the centroid to the vertex define three smaller triangles.

When we add in the segments from the centroid to the midpoint of each side we are actually finding the median of those three triangles.

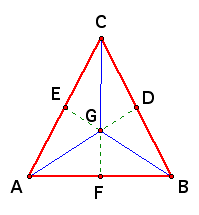
That means that those three triangles are each being split into two triangles of equal area. Now we know that

Our final step is to use what we know about triangles of equal area and to see larger triangles as being composed of several smaller triangles to gain our desired conclusion. With the medians of the large triangle ABC we were able to find that

From the picture we see that

Using that area(AFC)=area(BFC) we get that

Then using substitution for known equivalent areas we get that

Combining like terms then leads us to

and so

Now we have a string of equivalent areas

All that is left to show is that any of those four areas equals either area(AFG) or area(BFG). This can be done by looking at the picture of our triangle with its medians to see that

Since area(CDA)=area(BDA) we get that

Again we are going to substitute areas that we know are equal to get that

By combining like terms we know have

and so

Now we have the final string of equals areas

The medians of a triangle form six small triangles, each with area the is one-sixth the area of the original triangle.

To begin this have a given triangle.

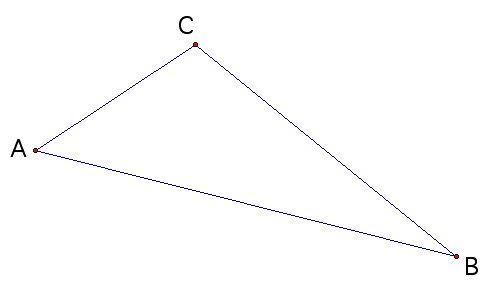
There is one and only one line that goes through A and is perpendicular to the line segment AB. Draw this perpendicular line and take it to be your y-axis. Then the line going through the points A and B can be taken as your x-axis. This is convenient because we can now label the vertices using the familiar rectangle coordinate system.

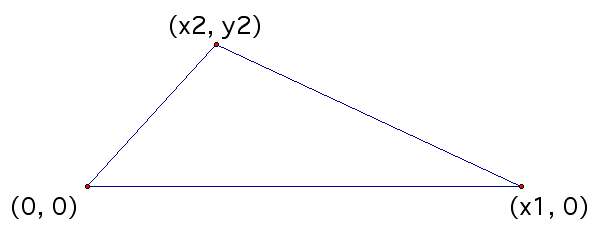
The notation we are currently using on the triangle feels very cumbersome and is not easy to work with. Keep in mind that labeling a distance as "x" is an arbitrary letter. We can use any letter that we want as long as it is able to take on all possible values for that distance. That means we can even label it as things like "2a" because when a is allowed to be a decimal then 2a can take on every real number value. This will be a much easier notation to work with in doing this proof, especially due to all the midpoints that will be taken. Here is our triangle with the new labeling system.

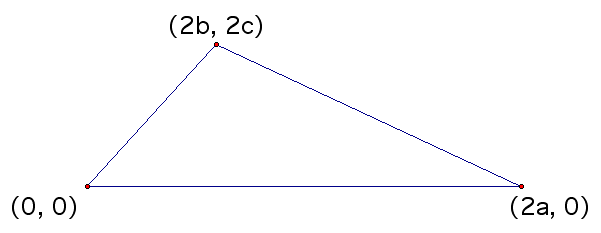
Please note that neither a nor c can equal zero because that would result in a degenerate triangle.

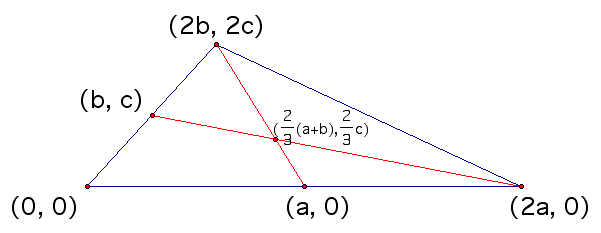
Trying to work with all three medians at one time is too difficult because at this point we don't even know for sure that they intersect in the same place. Therefore, we are going to draw in two of the medians, check that they intersect and if so find their intersection point. We will repeat that work for a different pair of medians. If the intersection point for both pairs are the same then we will know that all three medians meet at a single point. We begin by drawing two medians on our triangle.

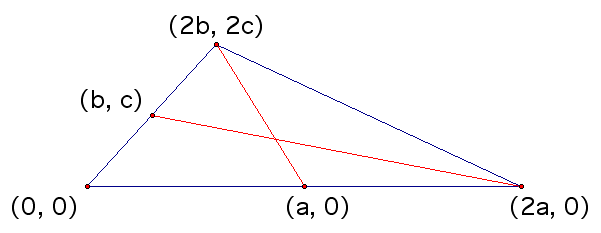
The coordinates for the midpoints were found using the familiar midpoint formula 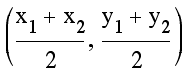which is used to find the point equidistant from and . When exploring whether the two medians currently present will interesect consider the lines that are constructed by extending these segments. Those two lines will not interesect if and only if they are parallel. Those lines are parallel if and only if they have the same slope. We can prove that they will interesect by finding the slopes of the lines using the points which define the medians. The slope equation is 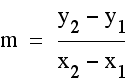and that gives us our two slopes of 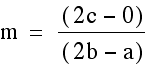and 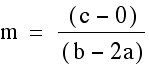. In order for the lines to have equal slopes it must be true that

When we distribute through we get the equation

By gathering like terms we see that to have parallel lines

must be true. That statement is only true if a=0 or c=0. However, we already stated that those values were not allowed because they resulted in degenerate triangles. Therefore, the lines formed by the medians of a triangle are not parallel and so they must intersect at some point.

To find out where those two lines intersect we must find the equations of the lines and then find their intersection point. We can find the equations of the lines using the point-slope form. This is convenient because we already determined the slopes of each line and we of course have points which the lines go through. The two equations of the lines are 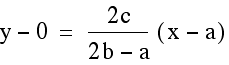and 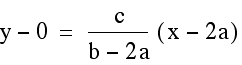. To find the x coordinate of the intersection point set these two equations to be equal to each other and then solve for x.

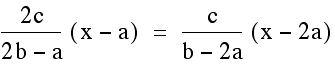
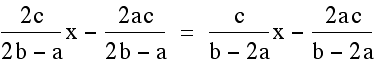
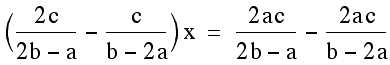
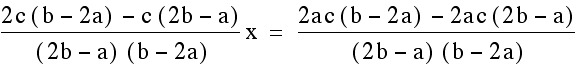
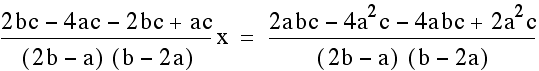
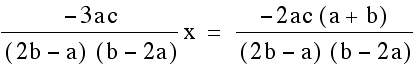
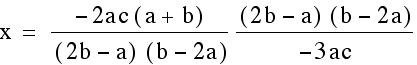
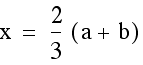
Once we find the x coordinate of the intersection point we can plug this either equation to find the y- value. This time we will plug it into both equations to verify that indeed we get the same y-value so we are finding a single point that lies on both lines.

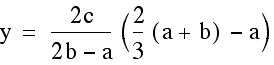
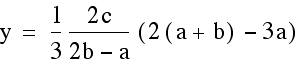
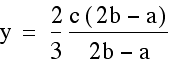
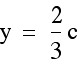
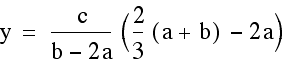
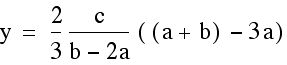
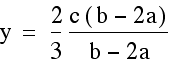
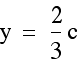
Indeed, the point 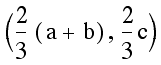lies on both lines determined by two of the medians of our triangle.

The next step is to repeat these procedures for a different pair of medians.

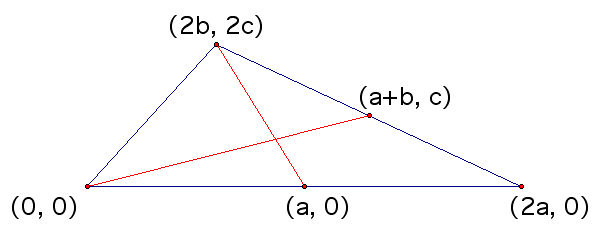
It is left as an exercise for the reader to verify that the lines determined by this pair of medians are not parallel and that they are defined by the equations 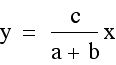and 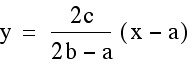. Now we can the point of intersection for these lines using the same methods as before.

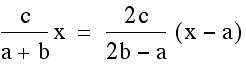
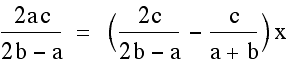
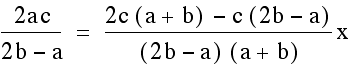
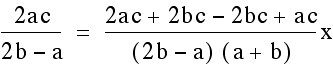
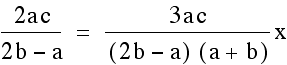
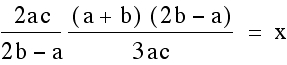
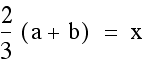
Notice that we do end up with the same x coordinate for the intersection point of this pair of lines. Since the line 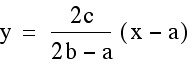was being intersected in both pairs we know that the y coordiate is going to have to be the same for this point since the x coordinate did not change. Therefore, the point 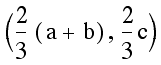lies on all three of these lines and is a common point of intersection. Notice that this point always lies on the inside of the triangle since it falls between the two of the x values, a and b, and between two of the y values, 0 and c. It is the common point of all three medians, i.e. the centroid.

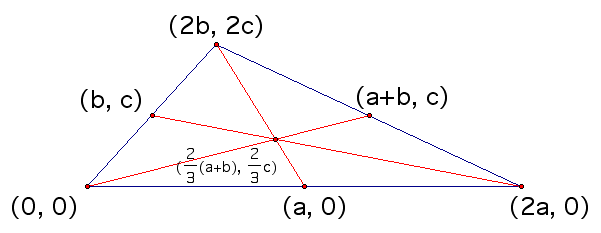
The final characteristic about the centroid that we are going to explore is that it cuts each of the medians in a 2:1 ratio. That means that the distance from the centroid to a vertex is twice as long as the distance from the centroid to its respective midpoint lying on the same median. To show this we are going to simply use the distance formula 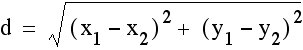. The reader is encouraged to verify the following table has the correct distances between the stated points.

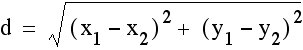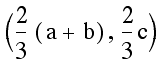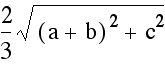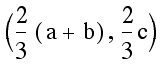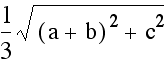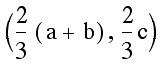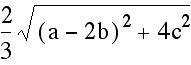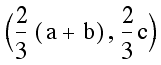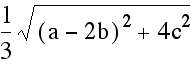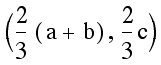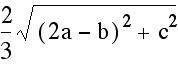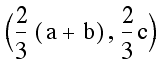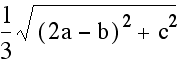It should now be clear that on each of the medians the distance from the centroid to the vertex is twice that of the distance from the centroid to the midpoint.

Triangles are a very rich subject with many interesting consequences. What happens if the midpoints on the sides of a triangle are connected? Can you find any relationship between the original triangle and the one formed by the connected those midpoints? What about if a triangle is formed using the medians as the sides of the triangle? The reader is encouraged to explore such topics in order to get a better understanding of the characteristics of the triangle.

Return