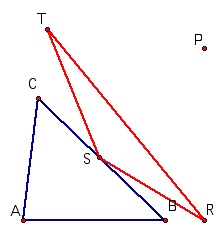
Triangles show up all over the place, as you may have noticed. Not only do they show up naturally and then we can do countless investigations with them, we can also construct new types of triangles. In this investigation we are going to be looking at Pedal triangles that are determined by a Pedal point. What are these things? What is so special about them? Read on to find out.

Let's begin by learning how to construct a Pedal triangle. Start with any triangle and any point in the plane. It will be to your benefit to construct your triangle with lines instead of segments because, like the orthocenter, we will be working with perpendiculars that do not always intersect at the segment.
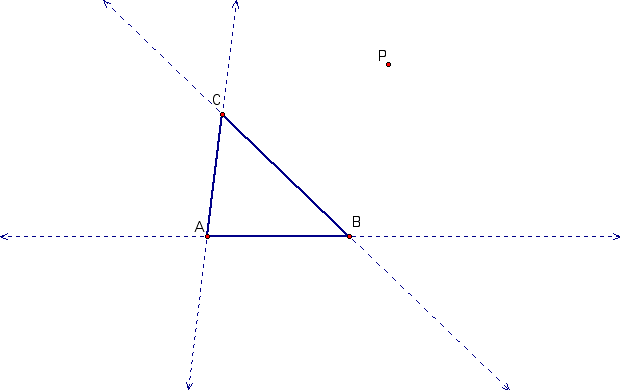
Draw in the lines that are perpendicular to each line that determines the triangle and go through the point P. Mark the points of intersection between your constructed lines and your triangle lines as R, S and T.
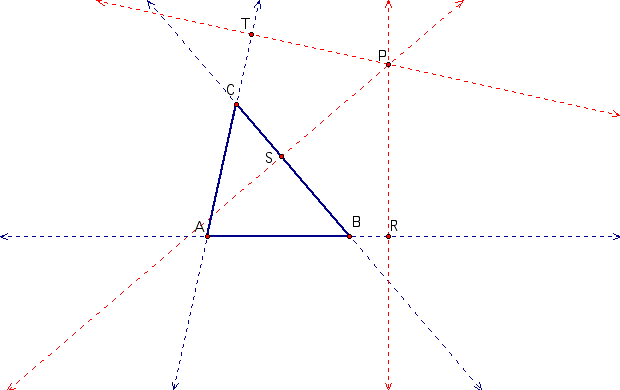
Finally, connect R, S and T to form a new triangle. This is your pedal triangle. The point P is your pedal point.
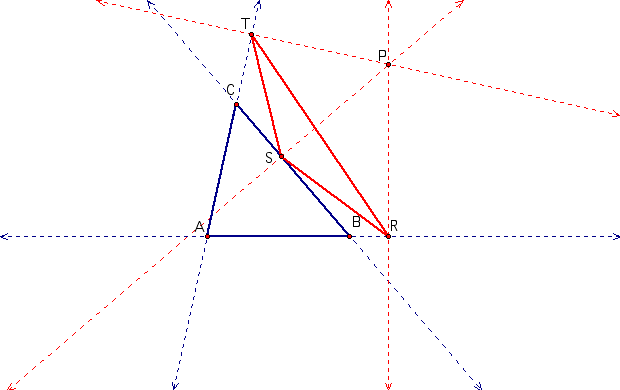
You can go here to try and construct a pedal triangle and point yourself. There is also a tool so that you construct a pedal triangle anytime you need one. Look at what happens when the Pedal point is a special point such as the circumcenter, centroid, a vertex, on the triangle ect. See what happens.
One thing you might have noticed is that when the Pedal point lies on the vertex the triangle degenerates to a line. This line is known as the Simson line. What we want to explore is when exactly does that happen. When are those three special points of intersection colinear? To explore this perhaps trace the Pedal point as you try to move it around the plane, keeping the triangle as degenerate as possible. We already know that the vertices are places we can go to give us a degenerate Pedal triangle and so we have some direction of how to do this.
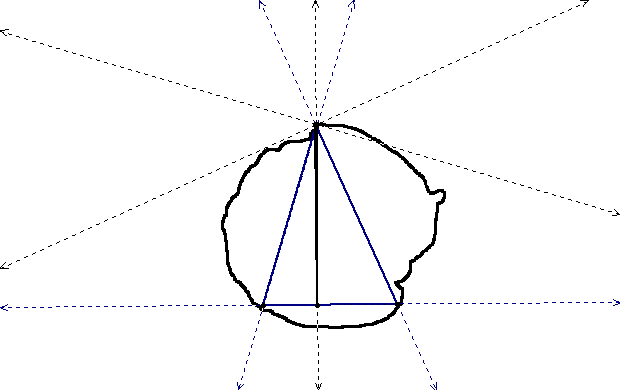
Even though this picture is by no means beautiful we can get the idea that it appears that when the Pedal point is on the circumcircle we get a degenerate Pedal triangle. Let's try to prove this.
Start with a triangle, its circumcircle and a point on its circumcircle.
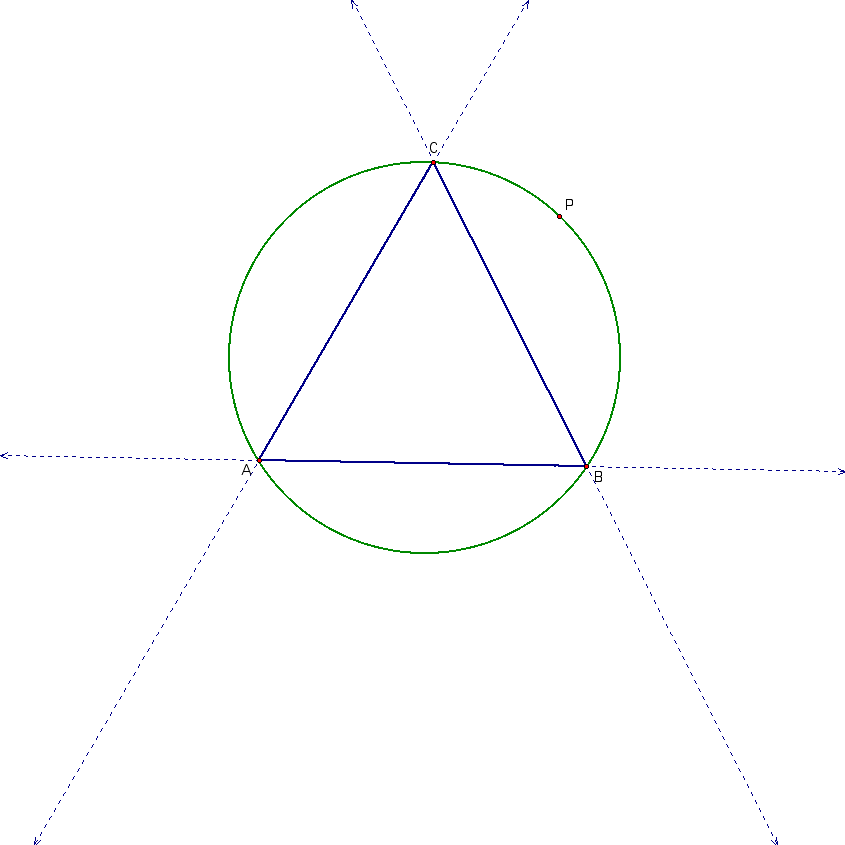
Go ahead and draw in the perpendicular lines that will define our pedal triangle as well as what we are hypothsizing to be our degenerate Pedal triangle aka the Simson line.
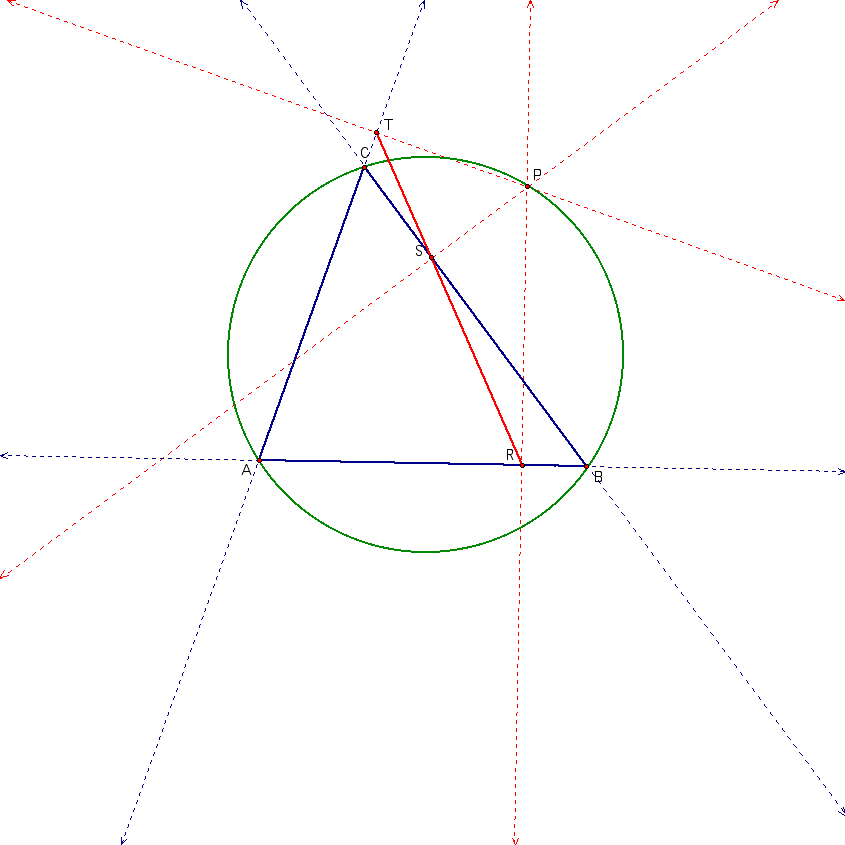
Notice by construction the points A, B, C and P all lie on the circumcircle. Let's connect those points to form a quadilateral.
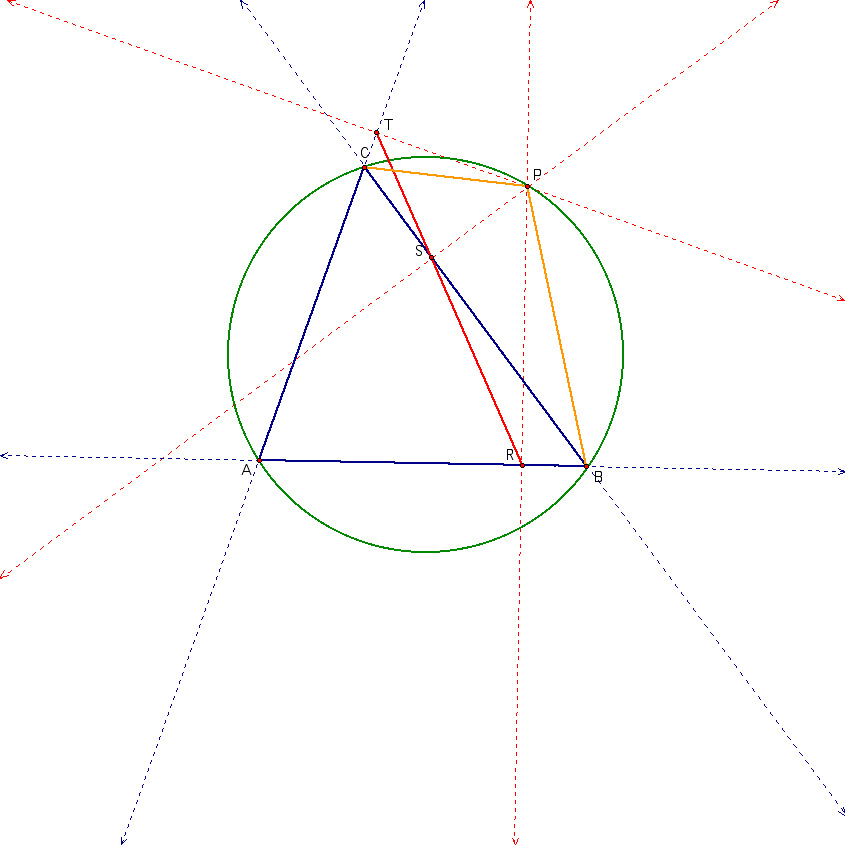
"Why should I do this?" you might ask. The reason we are doing this is because our quadrilateral is known as cyclic, since the vertices lie on a circle. Cyclic quadrilaterals have a very nice property indeed that will help us with our proof. The sum of opposite angles is 180 degrees. See the picture below for a proof of this claim.
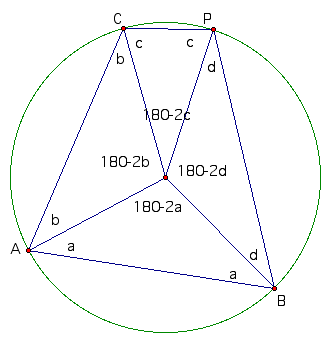
From the picture and some basic geometric knowledge we know that
Voila! Now we know that in our original picture
Look at the picture again.
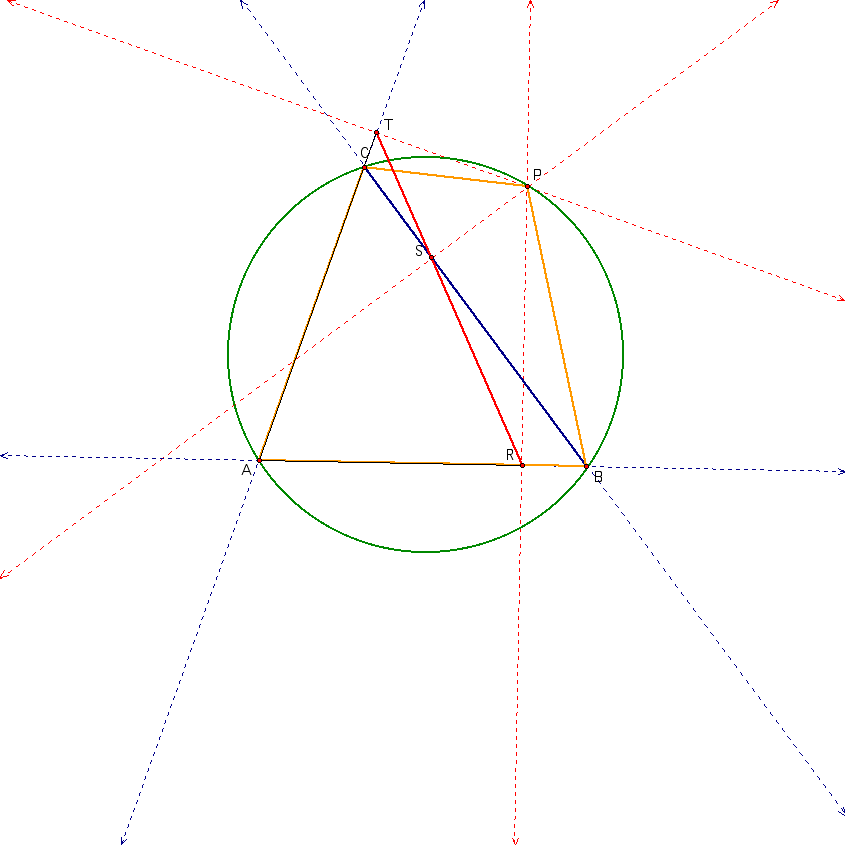
Notice that since the angle ARP is a right angle then the circumcircle for the triangle ARP is going to be one with diameter AP centered at the midpoint M. Likewise, the angel ATP is a right angle and its circumcircle for the triangle ATP is going to be one with the diameter AP centered at the midpoint M. But those are the same circumcirlces! Therefore A, T, P and R must lie on a single circle making the quadrilateral ATPR cyclic. That's just great because now
Since the points A, C and T are colinear and A, R and B are colinear angleBAC=angleRAT. Making that change and combining what we found above we get
Therefore
Using similar arguements you should be able to see that the quadrilaterals RSPB is cyclic.
Now we are going to look at another property of cyclic quadrilaterals when one of the sides is the diameter of its circumcircle.
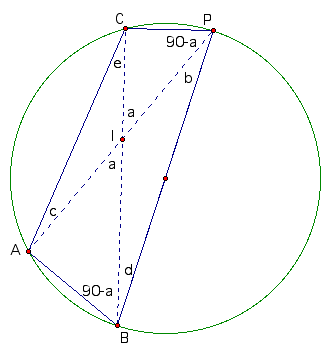
Notice that the angles BCP and BAP are right angles and that was used in filling out some of the angles. Adding up opposite angles gives us
and
Now let's look at the triangle ABC to get
and at triangle BCP to get
Now use the transitive property to combine the equations that we just came up with
and
Cool. Now let's use these results back at our picture
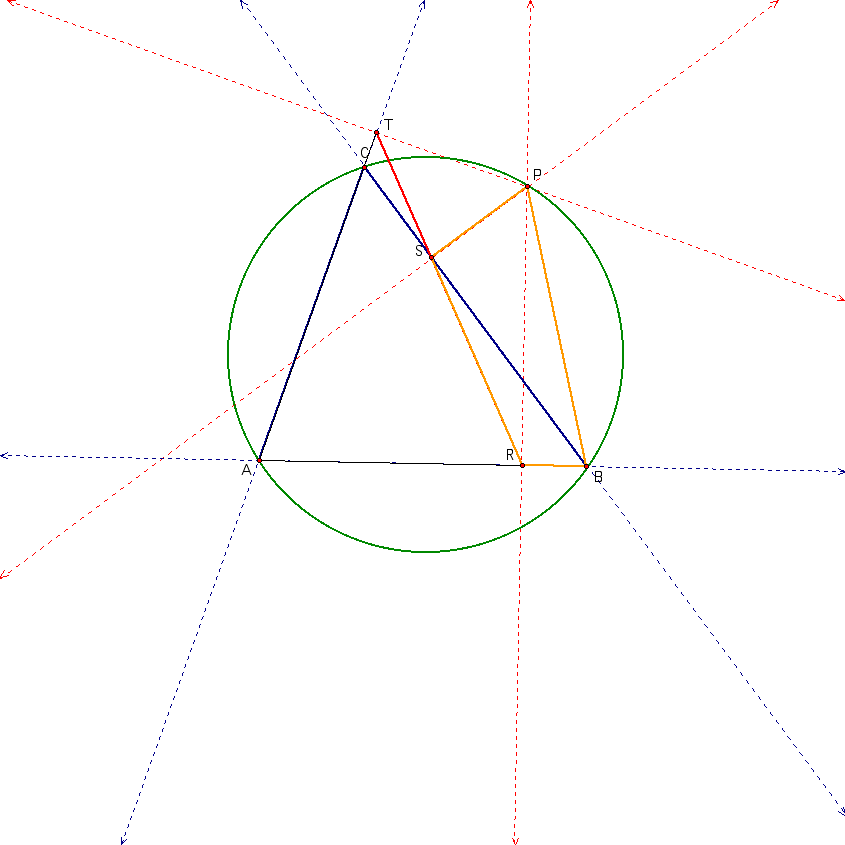
We can now say that
The proof will be wrapping up soon. There is just one more way that we want to look at our picture, focusing on yet another cyclic quadrilateral (why?) with its second diagonal and circumcircle drawn in.
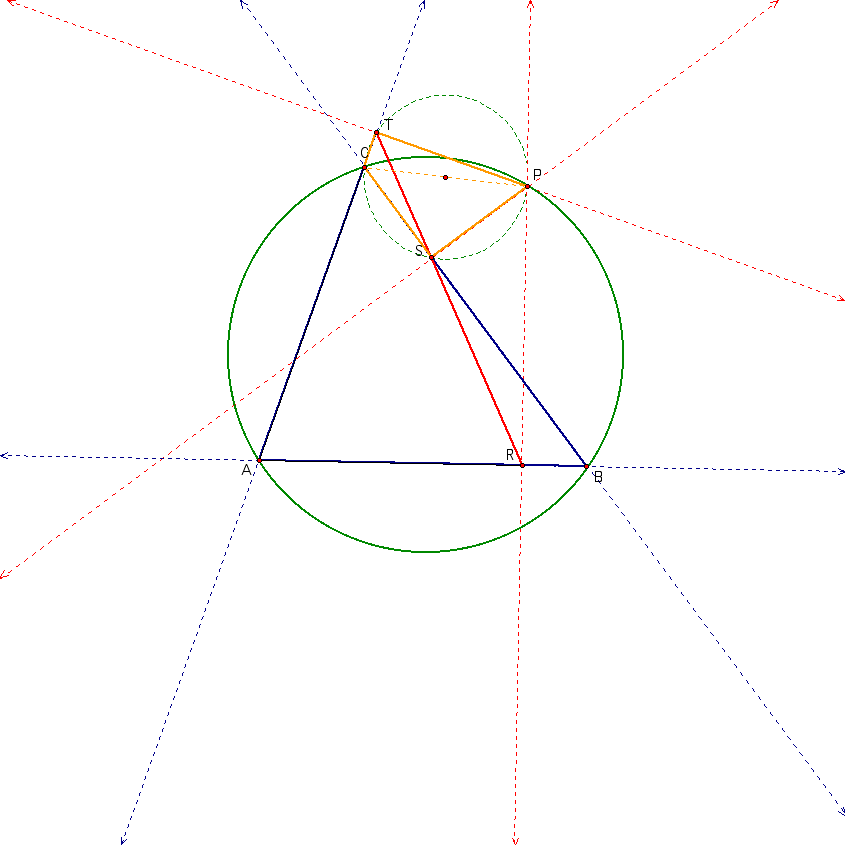
In this picture
You might wonder, why? This fact falls from several small geometric theorems on the behavior on angles in a circle. Please go to an extremely helpful pdf file here to read about why my claim is true. Now we can get down to the meat of this proof. From above we know the following statements are true
Now we just make a chain of equalities to get a very nice result
This is so nice because if angleCST=angleRSB
is true that means that they are vertical angles which implies
that R, S and T are colinear as desired!
A lot of stuff was done in the lesson that may have been difficult to follow on the screen. You are encourged to do each of the small proofs first and then to use those results to complete your main proof. Work the proofs on paper to make sure you have a good understand of the logic that is being followed. Do you see other relationships that are held in the context of a cyclic rectangle? Now that we know the Simson line exists when the Pedal point is on the circumcircle of the triangle, is the converse true? Will we only get a Simson line if the Pedal point is on the circumcircle? What happens if you trace the Simson line as the Pedal point moves along the circumcircle? So many fun questions, so little time.....