
When a line intersects a circle in only one point that line is said to be tangent to the circle. An interesting characteristic about the tangent line to the circle is that is always perpendicular to the radius that goes through the point of tangency. As a challenge to the reader try to verify this claim. The purpose of this assignment is go further in this topic. We want to find common tangent lines of two circles. If at anytime, while reading this investigation, you want to try these constructions yourself or explore ideas of your own, scroll to the bottom for a link that will take you to Geometry Sketchpad.

In solving this problem there are several cases that must be considered. In fact there are two different types of tangent lines that we are looking to construct based on each of the said cases. The two types of tangent lines are internal tangent lines and external tangent lines. An internal tangent line occurs when the common tangent line intersects the segment which connects the center of the two circles.
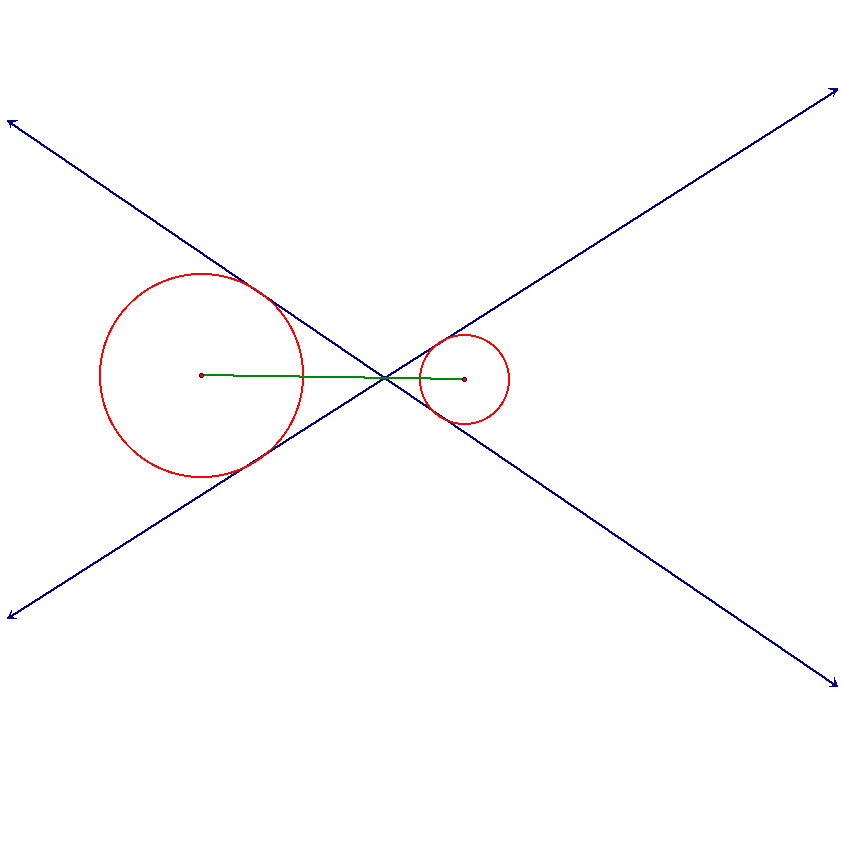
An external tangent line occurs when the common tangent line does not intersect the segment which connects the center of the two circles.
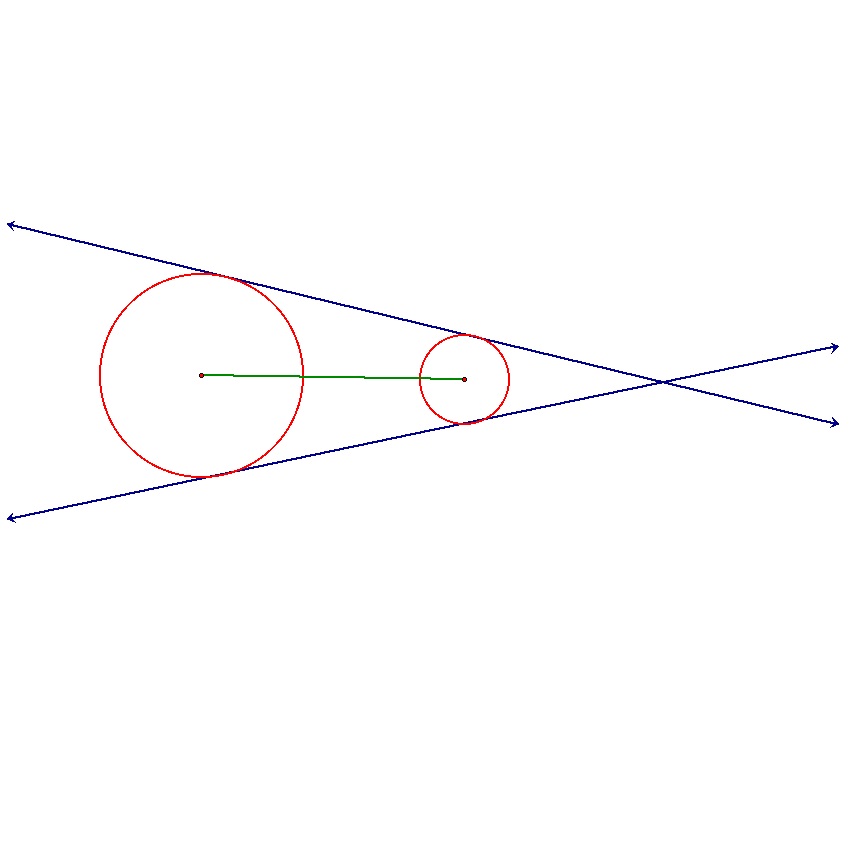
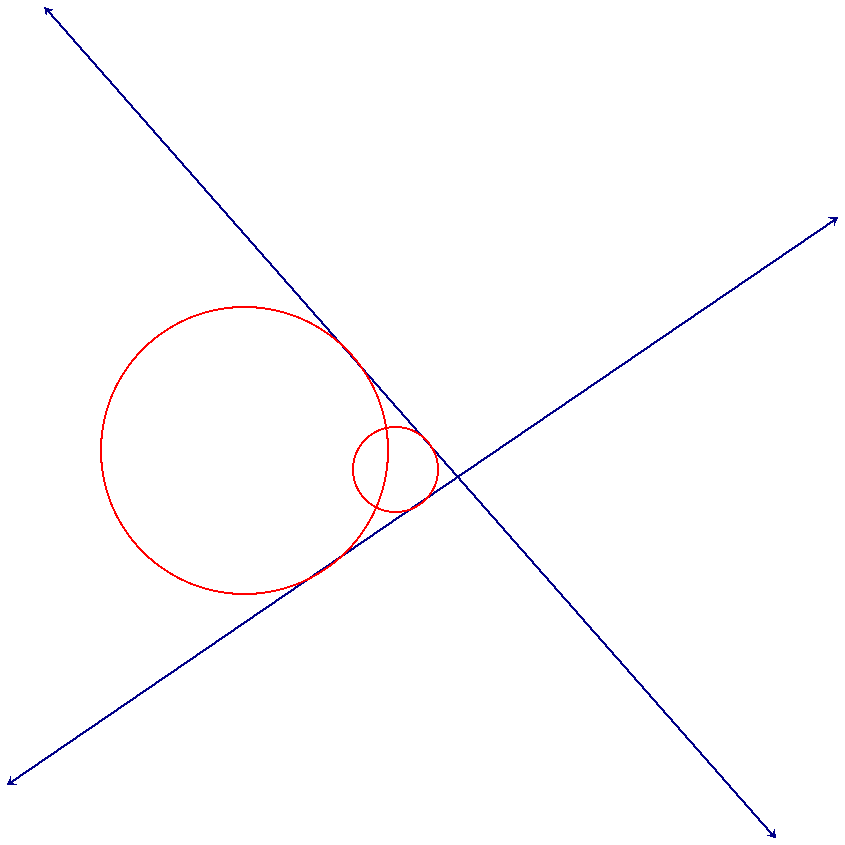
There are three ways which two circles can interect: in zero, one, or two points. If they intersect in zero points then it could be that one is contained in the other circle and they cannot have any common tangent lines.

It also could be the case that they are merely disjoint circles which would result in a pair of internal tangent lines and a pair of external tangent lines.
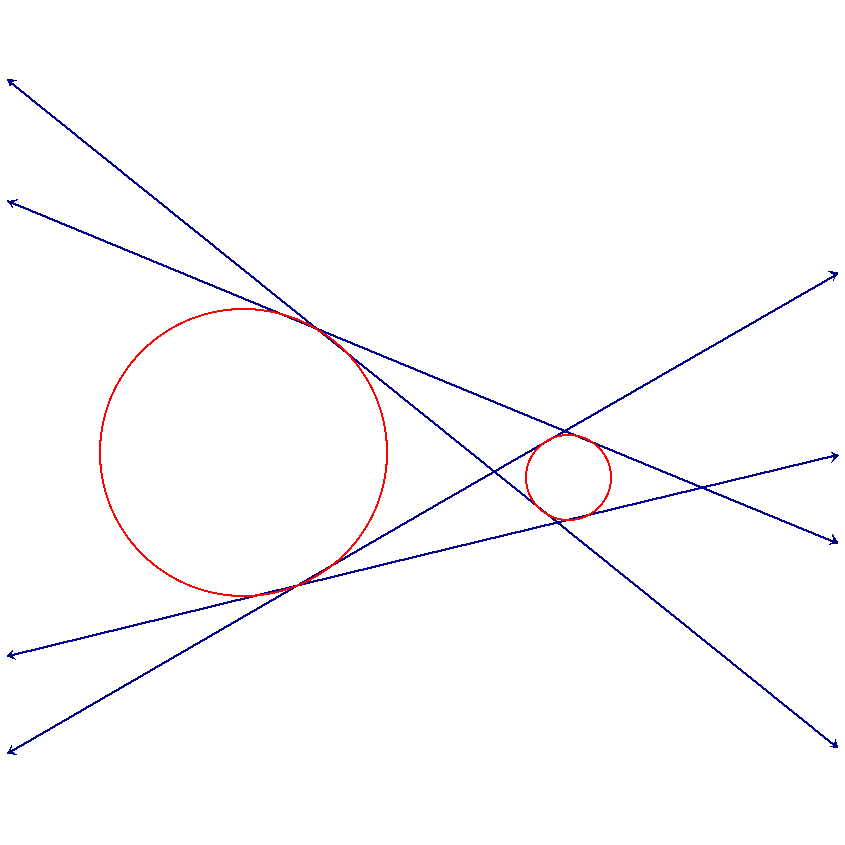
If they intersect at one point then they are tangent to one another. One of their common tangent lines will occur at their point of intersection.

In this case there will also be a pair of external tangent lines.
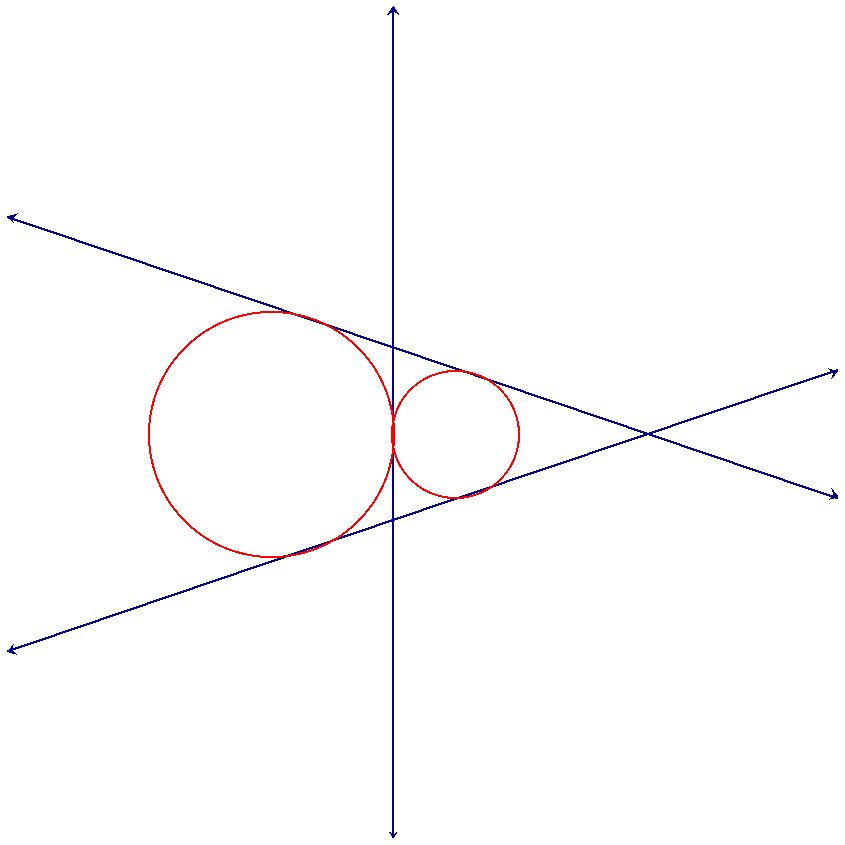
We can also have the case that the circles intersect in two points. Since the definition of internal tangent lines is that it goes through the segment joining the centers of the circles and that segment in contained inside the union of the circles there cannot be any internal tangents lines. Therefore, this case will result in a single pair of external tangent lines.
Notice that in each of the pictures above our two circles are different sizes. When the circles are the same size is a degenerate case and must be tackled seperately when doing the construction. It does NOT affect the number or types of tangent lines. It only affects how those tangent lines must be constructed. When we learn about how to construct the tangent lines keep in mind that circles of equal sizes are degenerate cases and try to understand why that is and what needs to be done differently to construct their tangent lines.
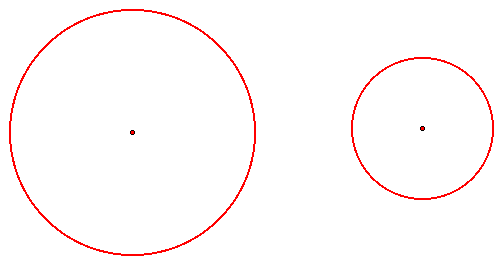
In order to construct the line tangent to two circles start with two circles. For clearness of the construction we are going to start with two disjoint circles, neither circle contained in the other, of different sizes.
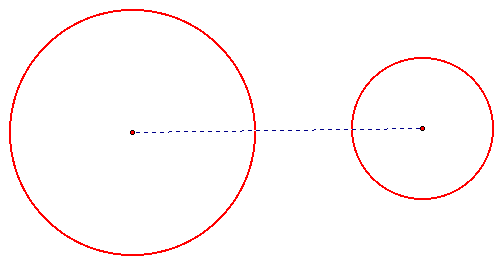
Of course the tangent line is going to be a function of how far away the circles are from one another so connect the circles with a segment.
Call the radius of the large circle r1 and the radius of the small circle r2. Construct a new circle of radius r1+r2.
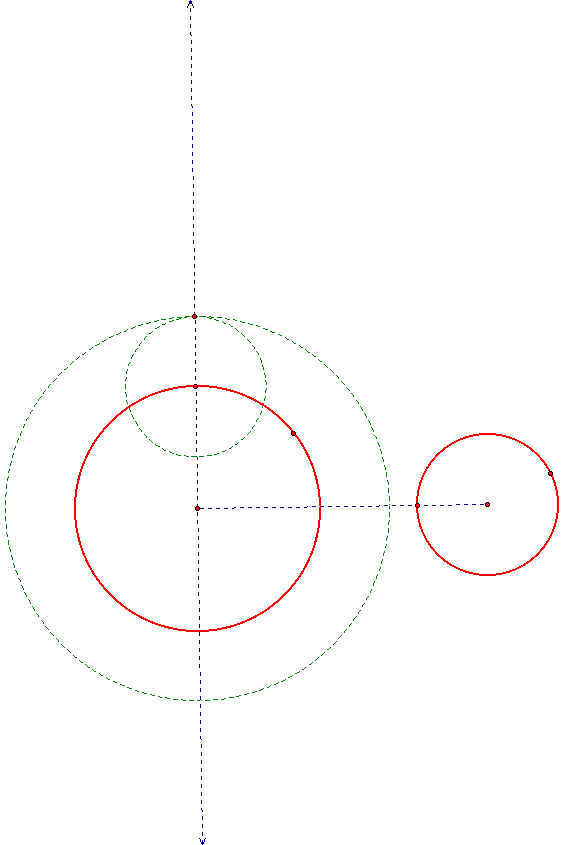
Now construct a circle that goes through the centers of the two given circles using the midpoint of the blue segment.
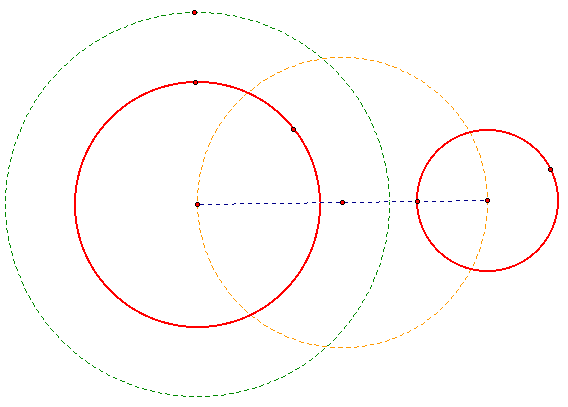
Construct a line through the top intersection of the green and orange circles and through the center of the large circle.

We have now found where the tangent line intersects the big circle. All that is left to do is construct a line at the point perpendicular to the blue line.

This gives us one of our internal tangent lines. Repeat the some construction except this time use the bottom interesection point of the the green circle and the orange circle.
Notice that as the small circles gets closer and closer to the large circle the intersection points on the green and orange circles get closer as well. When the two red circles are tangent the intersection points of the green and orange circles collapse to one point. When the two circles have two intersection points the green and orange circles cease to intersect. Since that intersection is crucial in the construction of the internal tangent lines we see that circles with two intersection points have no internal tangent lines and circles with one intersection point will only have one tangent line. Can you see why we constructed the internal tangent line for two tangent circles seperately?

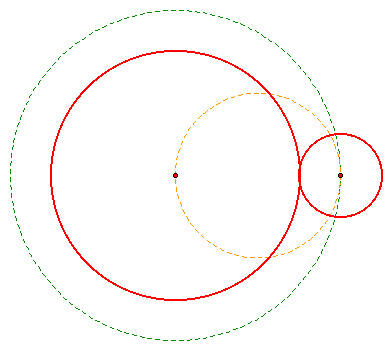
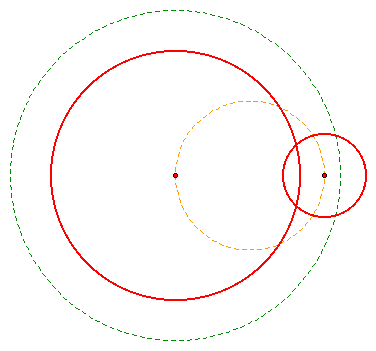
Now we are going to learn how to construct the external tangent lines to the same category of circles. The method is remarkably similar. Remember that we called the radius of the large circle r1 and the radius of the small circle r2. We are going to construct the external tangent lines using the same logic and steps that we used for the construction of the internal tangent lines except our green circle is going to be the circle with radius r1-r2 cocentric to the large circle instead of the circle with radius r1+r2 cocentric to the large circle.
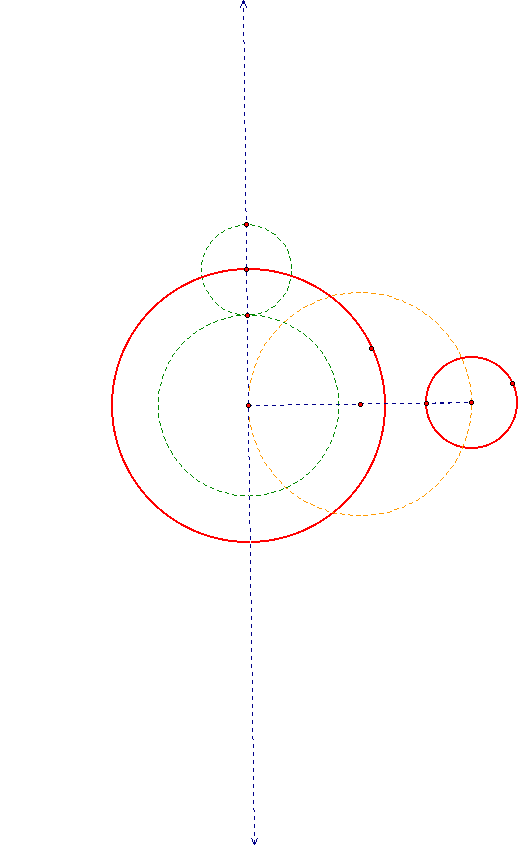
Now draw in the circle that goes through the centers of the given circles and construct lines that go through the intersection of that circle and the green circle and through the center of the big circle.
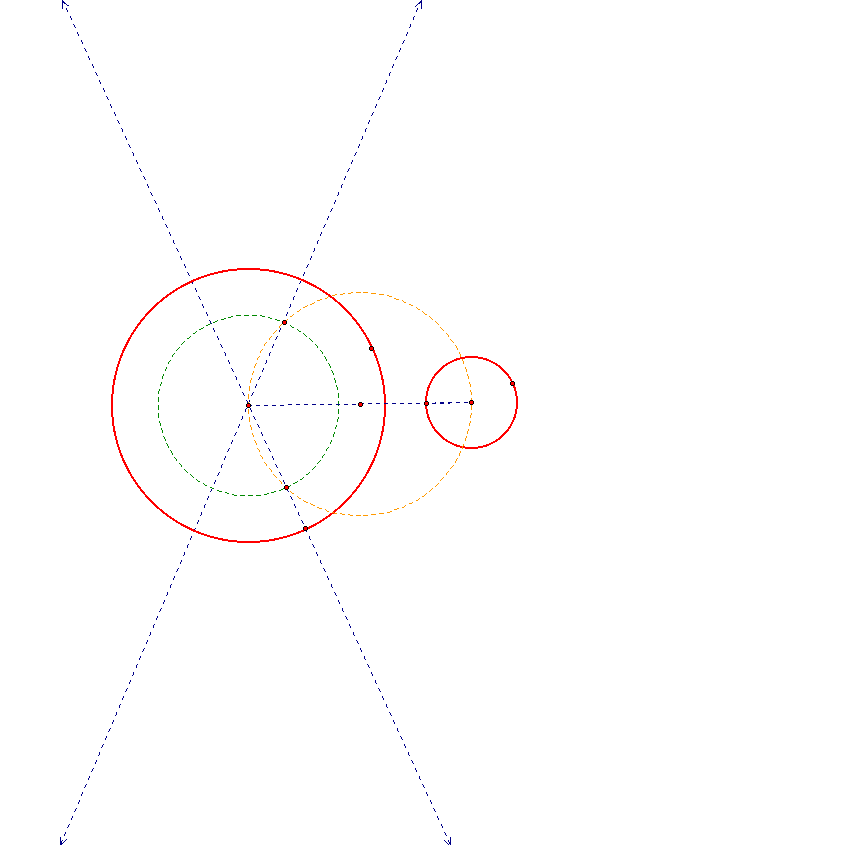
Finish up by constructing lines that go through the intersections of the blue line and the large circle that are perpendicular to the blue line.
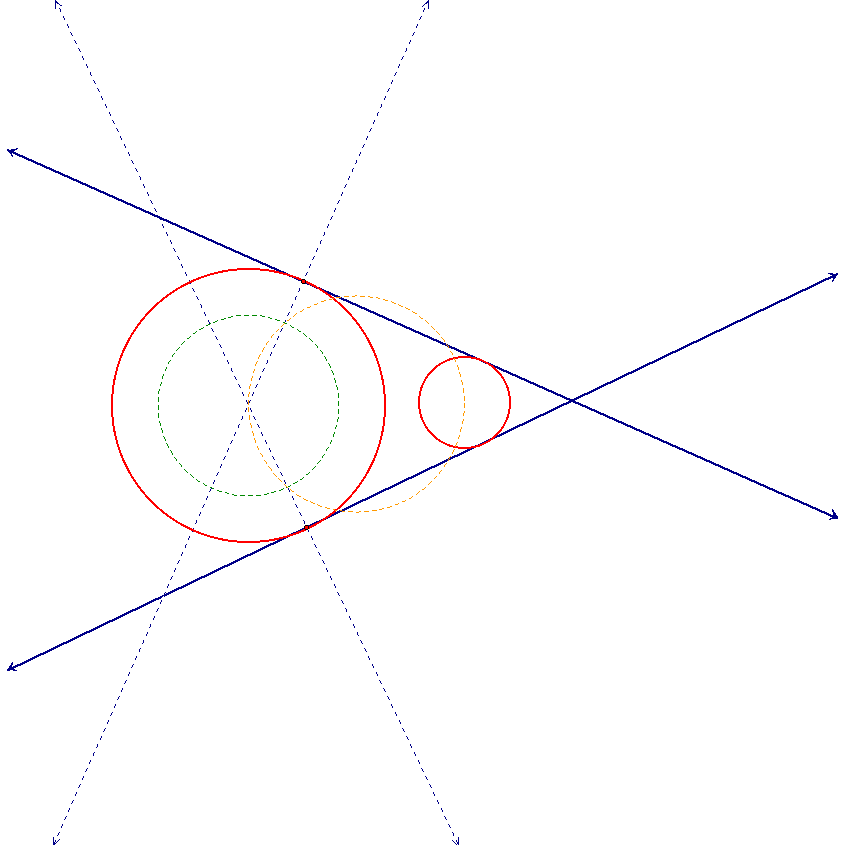
Now we have external tangent lines. Put them together and we have all of our common tangent lines for two circles of different sizes that are not tangent.
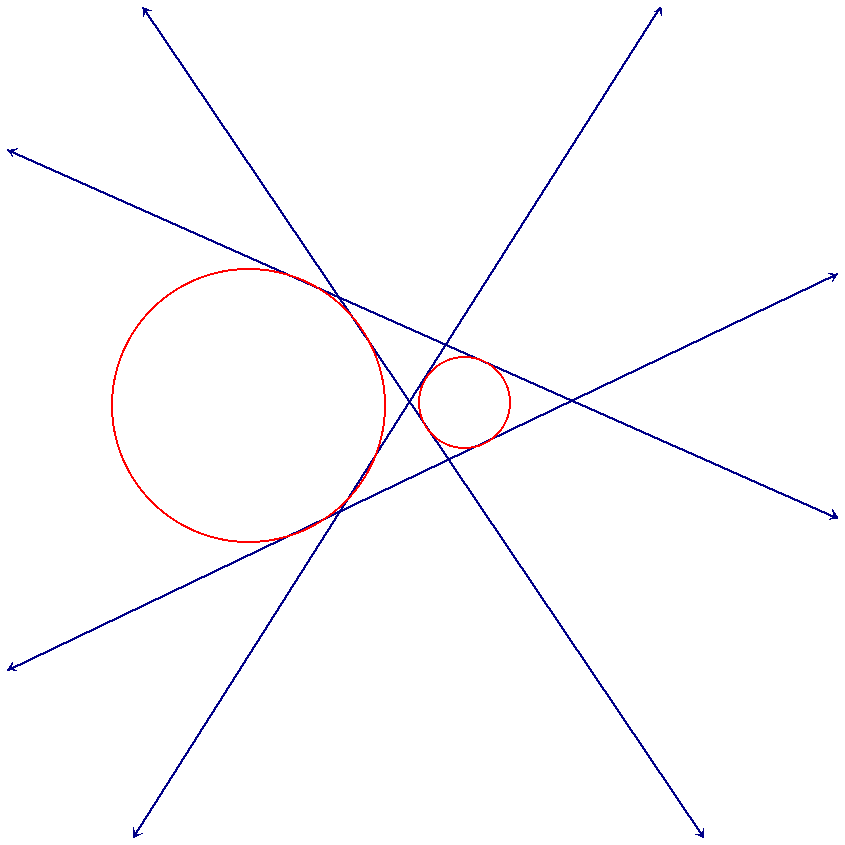
Notice that if the two circles were the same size then r1-r2 would be zero and so there would be no green circle with which to do this construction. That is why having two circles of the same size is a degenerate case. Let's go ahead and work out the other cases.
If the two circles are the same size and are not tangent their internal tangent lines can be constructed the same way as before. Only their external tangent lines need to the constructed differently. Connect the centers of the circles using a segment and the find the lines that are perpendicular to that segment and that go through the centers of the circles.
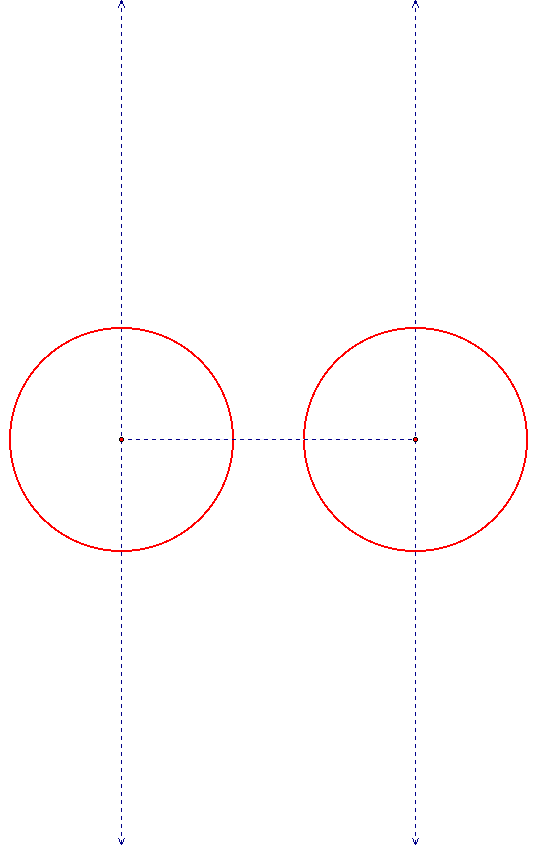
Now just draw the lines going through the intersection points of the blue line and the circles that are perpendicular to the blue lines. Can you see why this construction always leads to a tangent line?
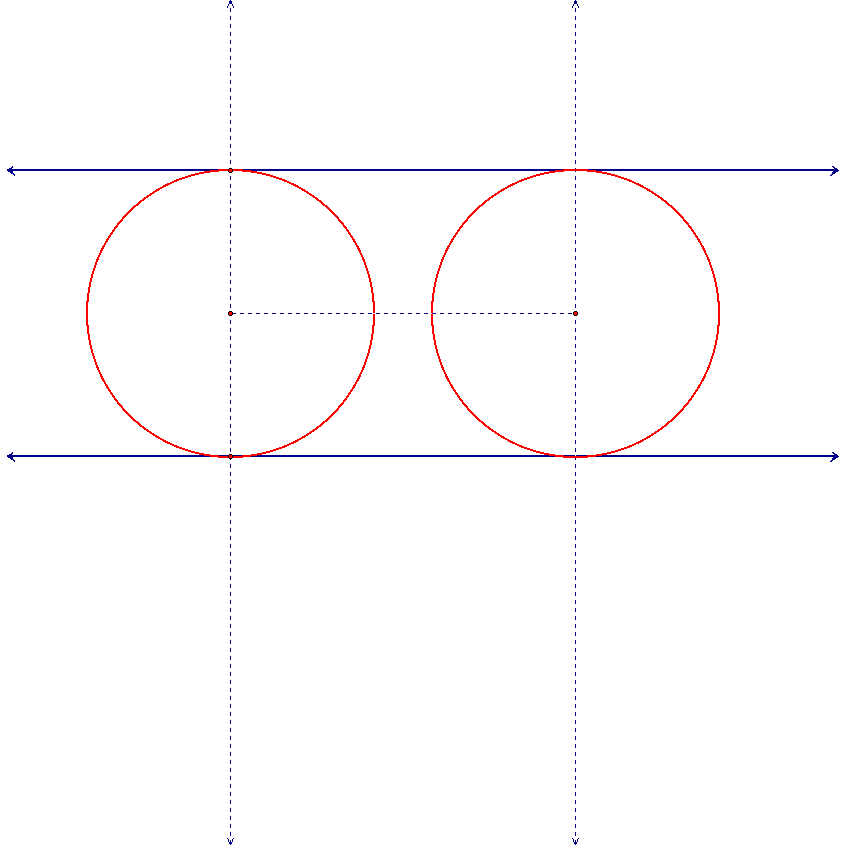
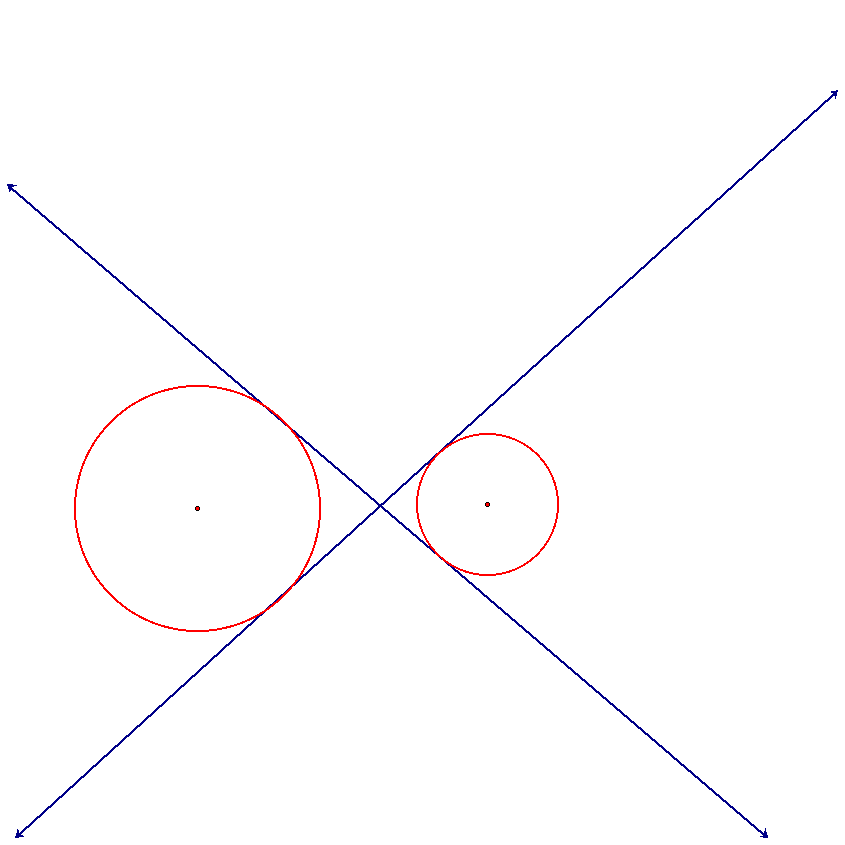
The final case that needs to be considered is when the two circles are tangent to one another. As discussed, the problem that comes in is when trying to construct the internal tangent lines. The external tangent lines can still be constructed using the methods of above, pay attention to whether the circles are the same size or not. The internal tangent line is going to be the tangent line that goes through the point of tangency and is perpendicular to the segment connecting the centers of the two given circles.
Now we know how to construct lines tangent to any two given circles. Go here and where tools for these constructions have been made based on the different cases discussed. It is suggested that when going to choose a tool click on "show script view". Because of the fact that these constructions are heavily based on which circle is large and which one is small the order in which you choose your points will make a difference in whether the tool works properly or not. There are notes in the script about how to properly use these tools. Try and make the constructions yourself so that you can really understand how this works. Try finding a line tangent to a given circle and going to through a given point not on the circle. Have fun with playing with different things you might see.