affects the graph of the respective
parabola. Now are we going to explore how varying just one of
the constants, b, can affect the solutions to 
.
These solutions are also known as roots of .During the assignment "Life of a Parabola"
we explored how varying the constants a, b and c in the equation
affects the graph of the respective
parabola. Now are we going to explore how varying just one of
the constants, b, can affect the solutions to .
These solutions are also known as roots of .
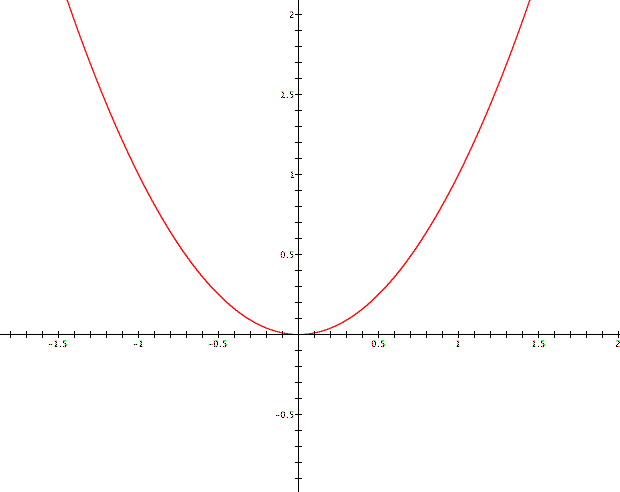
Since we are exploring the effect the b has
on the roots of a quadratic equation, begin by setting a and c
equal to 1. Then we are looking at the solutions of 
.
The following at the graphs of 
when
be is equal to -2, -1, 0, 1 and 2. Pay attention to where the parabola crosses the x-axis
because that is where y equals 0 and therefore where the roots
of the equation reside.
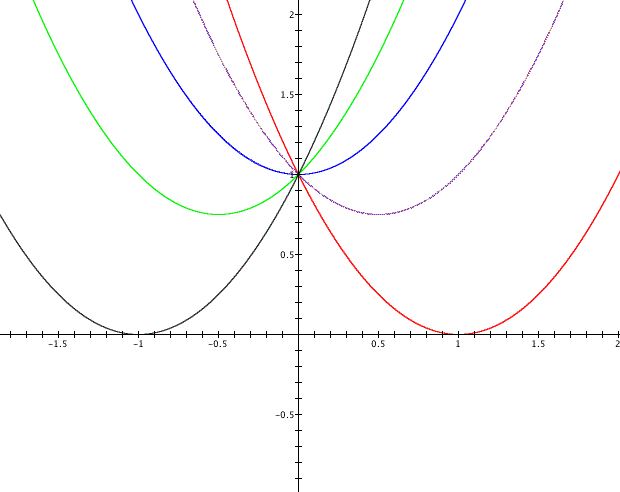
From the graph it appears that the equation only has a single root when b equals 2 and -2, because each graph only crosses the x-axis in one place, and no roots for the other values of b. From "Life of a Parabola" we know that if we continue to increase the value of b the parabolas will move in a curved downward direction. Let's observe when b equals -5, -2, 0, 2 and 5.
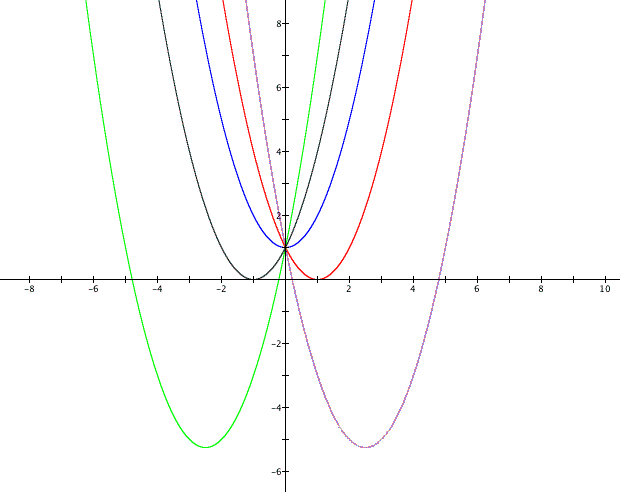
When b is either larger than 2 or less than -2 it appears that the equation has two roots since each graph crosses the axis in two places. A few natural questions about the effect of changing b are 1) how can we predict how many roots a quadratic equation has? and 2) how can we predict the x-values of the roots of a quadratic equation?
To discover how changing the value of b affects
the solutions to we are going to
plot this equation in the x-b plane. What that means is every
point of the graph below is an x value and a b value that gives
a solution to .
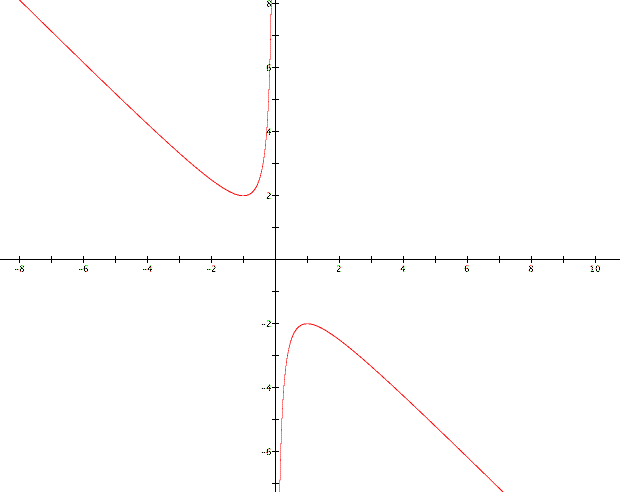
The way we determine how a value of b affects
the roots of the equation is
by choosing a value for b, say 3, and adding to the graph the
line b=3.
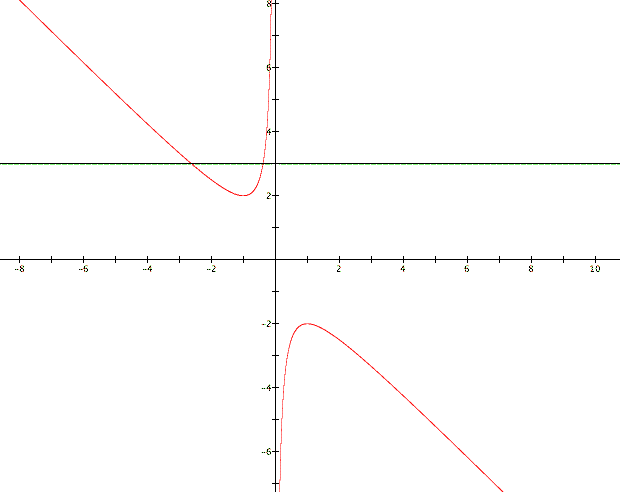
Observe where the two graphs intersect. The
x-value of those intersection points represent roots of the original
equation. What you are finding is a x value such that when it
is paired with your chosen b value becomes
a true statement. Earlier it appeared that
had two roots when b was less than -2 or greater than 2, one root
when b equaled 2 or -2 and no roots when b was between -2 and
2. Let's verify that by looking at our graph in the x-b plane.
In this graph we have b=-3, -2, 1, 2 and 3.
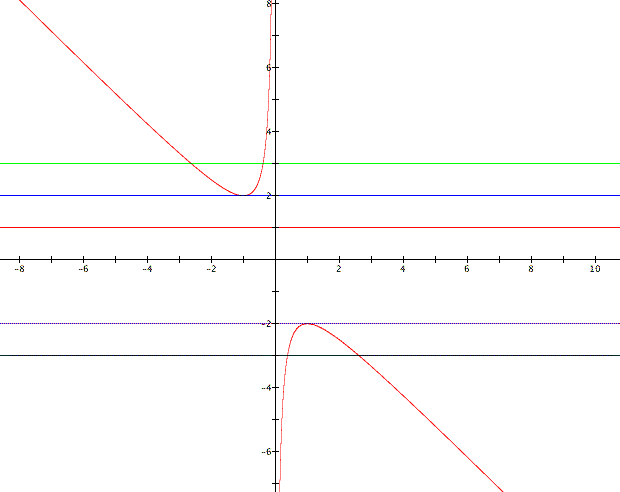
We have explored well,
but what happens if we change c from 1 to -1. Below is the graph
of 
, which represents this change,
along with the graph of so that we can
see what exactly has changed.
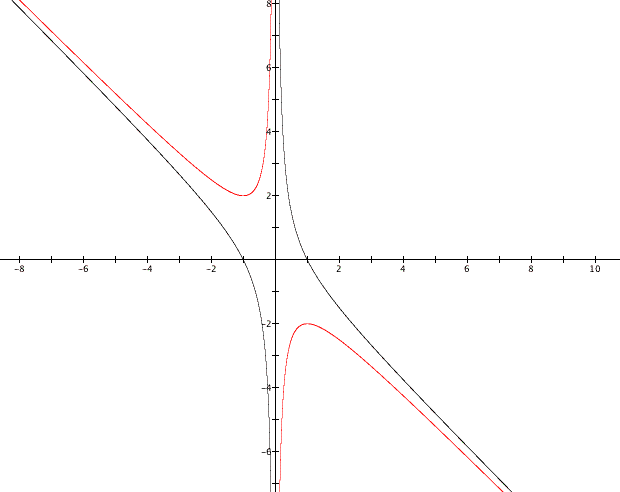
We see that when b is between -2 and 2 the change in c makes a very big difference in how many roots are possible. In fact, there are now always two roots for every value of b. Interestingly, as b grows up towards infinity and down towards negative infinity there seem to be a very small difference in the roots when c equals 1 and when c equals -1. Let's observe the graphs for c=-5, -3, 0, 3 and 5.
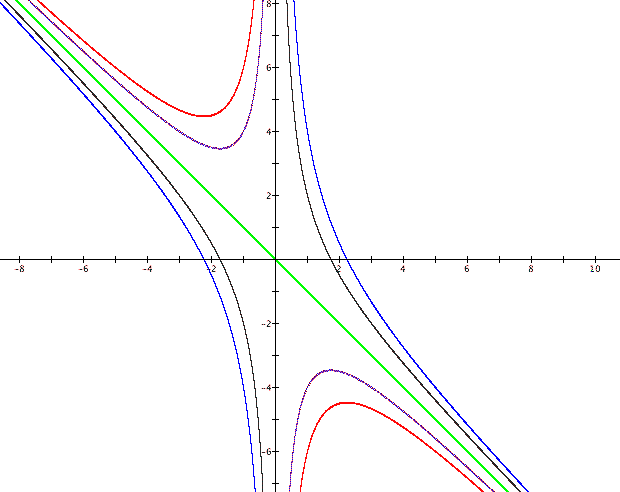
It appears that as b gets very large in the
positive and in the negative direction, the roots of 
limit to the same same roots when c equals zero, 
.