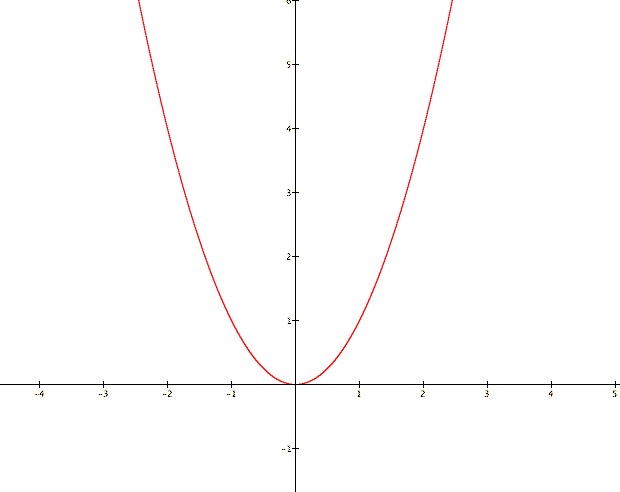
The parabola is a ubiquitous graph in mathematics. Although students recognize the familiar U-shape of the graph, many do not truly understand the nature of what they see and how a second-degree function works to determine the picture.

The general form for a second-degree equation,
or a quadratic form, is ![]() .
During this assignment we will explore what happens to the graph
when the constants a, b and c are varied. In doing so we will
strive to gain new insights about the nature of the parabola.
.
During this assignment we will explore what happens to the graph
when the constants a, b and c are varied. In doing so we will
strive to gain new insights about the nature of the parabola.
If we try to vary a, b and c at one time our graphs would be a mass of confusion. Therefore, we will fix values for two of the constants at a time and vary only the third. That means we will have three sets of graphs and discussions, one for each of the constants that is varied.
To begin fix a and b to be 1 and let's explore what happens as c varies. The following graphs are when c=-2, -1, 0, 1 and 2.
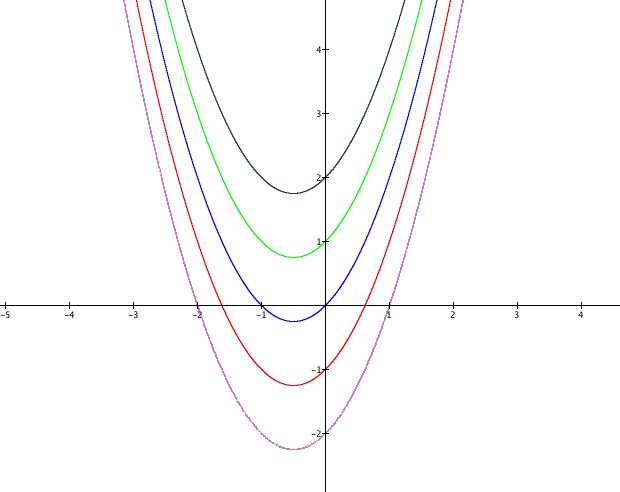
Two things should be noticed on these graphs.
1) The first is that the vertex appears to
be moving in a verticle direction as c changes. This makes since
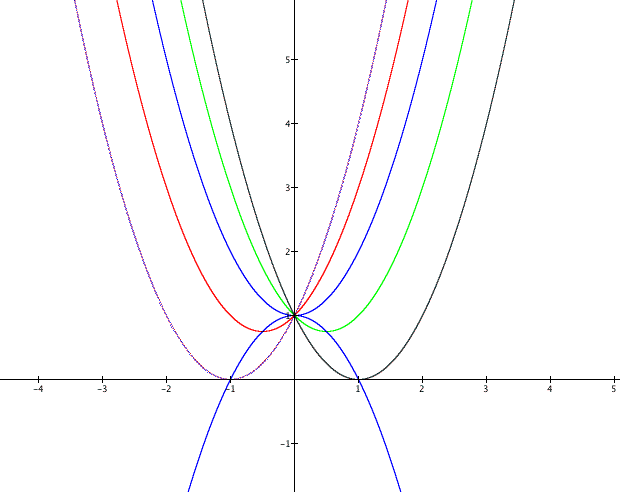
because a vertex on the parabola ![]() occurs at (
occurs at (![]() ,
,
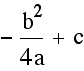 ). Specifically,
on the parabola
). Specifically,
on the parabola ![]() the vertex occurs at (
the vertex occurs at (![]() ,
,
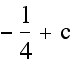 ).
).
Note: These coordinates for the vertex can be obtained from either completing the square or using derivatives.
Seeing what the coordinates for the vertex of a parabola are, it should be clear that it is only affected by c in the manner of a vertical shift of distance c.
2) The second important aspect of these graphs
is that the y-intercept appears to always be at (0, c). This makes
sense from the equation of the parabola being ![]() .
It follows immediately that when x=0, y=c. In fact, it follows
directly from the general form of the parabola as well,
.
It follows immediately that when x=0, y=c. In fact, it follows
directly from the general form of the parabola as well, ![]() . The
y-intercept will always be at (0, c) no matter what the values
for a and b are.
. The
y-intercept will always be at (0, c) no matter what the values
for a and b are.
Next, fix a and c to be 1 and investigate what happens when b varies. The following graphs are when b=-2, -1, 0, 1 and 2.
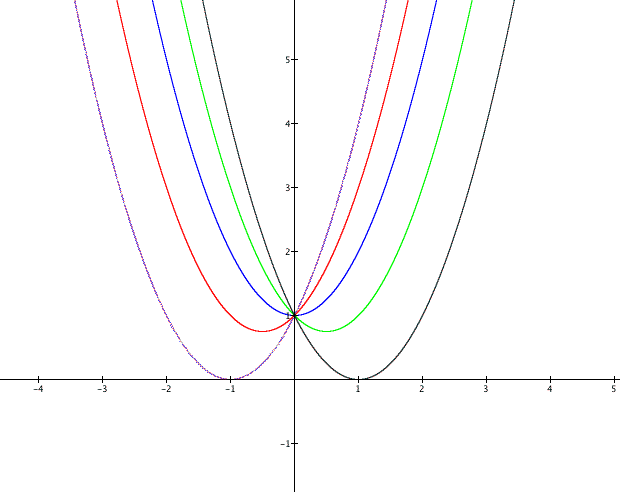
It appears that the graphs are traveling in a curved fashion. Imagine connecting the vertices together in a smooth manner. What picture do you see? Possibly it looks something like an upside-down, or inverted, parabola. We said before that that vertex of a general parabola is at
(![]() ,
,
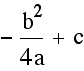 ). Since
a and c have been fixed at the value of 1 we now get the vertex
to lie at the point (
). Since
a and c have been fixed at the value of 1 we now get the vertex
to lie at the point (![]() ,
,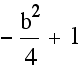 ).
With a little bit of simplification and grouping we get a very
convenient form of this vertex which is
).
With a little bit of simplification and grouping we get a very
convenient form of this vertex which is
(![]() ,
,
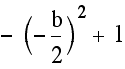 ). The
reason this is a nice form is that it is now possible to see that
the vertex always lies on the parabola
). The
reason this is a nice form is that it is now possible to see that
the vertex always lies on the parabola ![]() .
Although we derived this algebraically, let's verify our findings
graphically. This following graph has each of the parabolas as
the previous graph and the graph
.
Although we derived this algebraically, let's verify our findings
graphically. This following graph has each of the parabolas as
the previous graph and the graph ![]() as well.
as well.
Indeed it is clear on our picture that the
vertices of parabolas taking the form (![]() ,
,
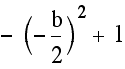 ) lie
on the graph
) lie
on the graph ![]() .
Even more generally, since the vertices of any parabola of the
general form
.
Even more generally, since the vertices of any parabola of the
general form ![]() take the form
take the form
(![]() ,
,
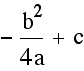 ), which
is equivalent to (
), which
is equivalent to (![]() ,
,
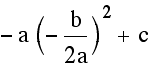 ). We
can deduce that when a and c are held constant the vertices of
). We
can deduce that when a and c are held constant the vertices of
![]() lie
on the parabola
lie
on the parabola ![]() .
.
Finally, fix b and c to be 1 and investigate what happens when a varies. The following graphs are when a=-2, -1, 0, 1 and 2.
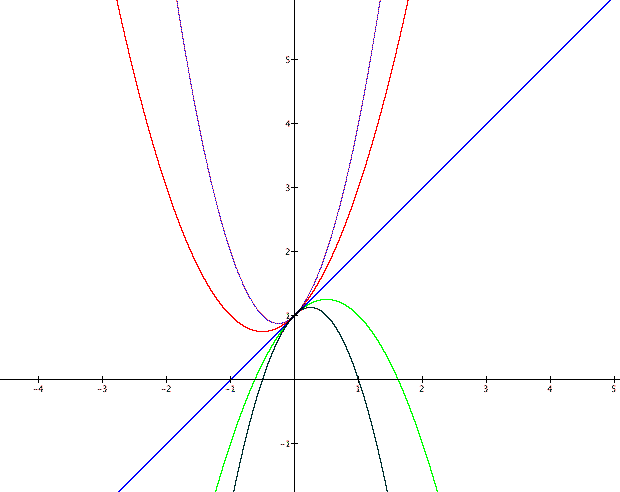
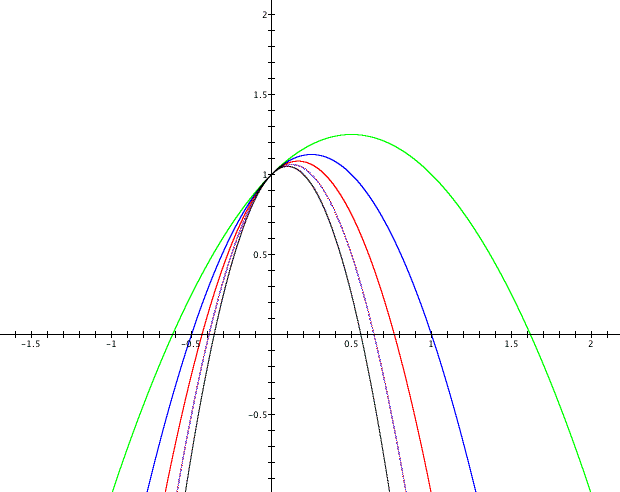
One characteristic of these graphs is that when a is negative we get a parabola that opens down and when a is positive we get a parabola that opens up. When a equals zero our equation is reduced down to a linear form so it is not surprising that the graph is a straight line. It appears that the value of a may also play a role in how wide the parabola is and where its vertex lies. To investigate this further let's look at two more graphs, one with several positive a values and another with several negative a values. The first graph is for a=-5, -4, -3, -2 and -1
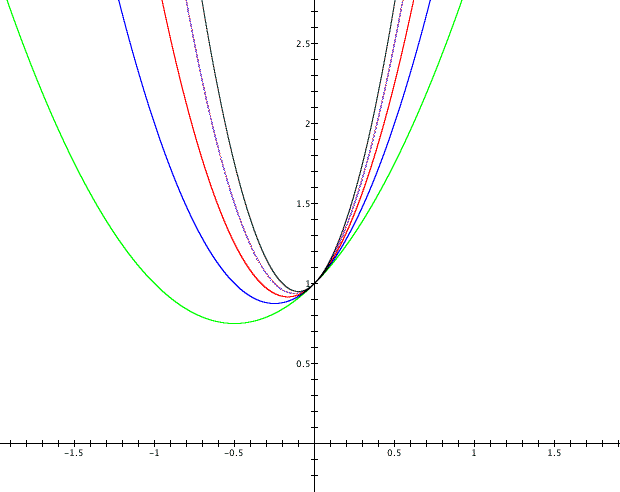
The second graph is for a=1, 2, 3, 4 and 5
This third graph is merely the fuctions present on the two previous graphs put onto a single graph.
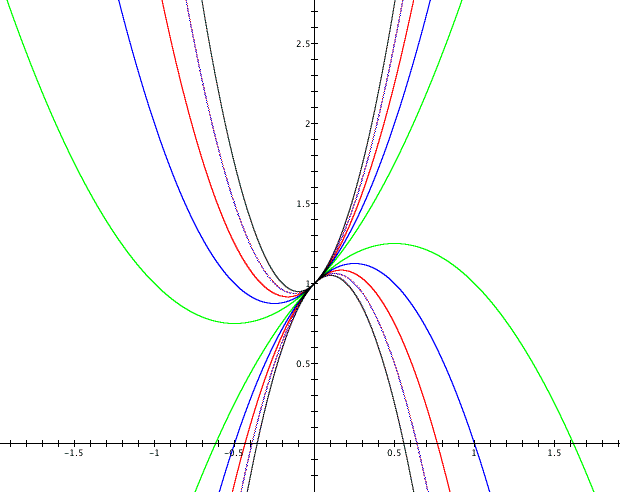
It does appear that the larger the magnitude
of a is, the skinnier the graph becomes. The vertices of the parabolas
also appear to be moving up and to the right in a linear manner
as a increases in value. We already discussed that the vertex
of a general parabola takes the form (![]() ,
,
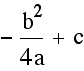 ). Since
our parabolas have the equation
). Since
our parabolas have the equation ![]() then each of the vertices have the coordinates (
then each of the vertices have the coordinates (![]() ,
,
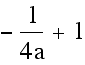 ). Again,
change the form of the coordinates in a convenient way so that
it is easier to deduce the equation of the function that predicts
the location of the vertices of our parabolas. That convenient
form would be
). Again,
change the form of the coordinates in a convenient way so that
it is easier to deduce the equation of the function that predicts
the location of the vertices of our parabolas. That convenient
form would be
(![]() ,
,
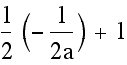 ) and
it leads to the equation
) and
it leads to the equation 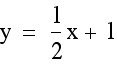 .
Below is a graph with all of the parabolas as above plus the line
.
Below is a graph with all of the parabolas as above plus the line
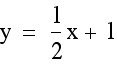 .
.
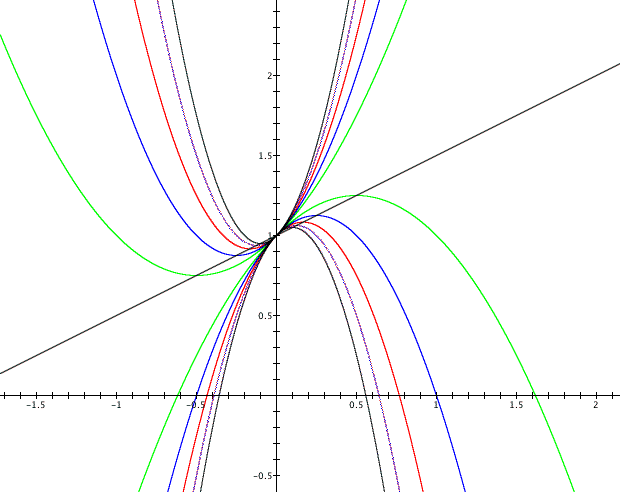
Now we can see graphically as well as algebraically
that the vertices of parabolas ![]() lie on the line
lie on the line 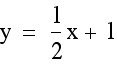 .
Even more generally, a parabola taking the form
.
Even more generally, a parabola taking the form ![]() has the vertex (
has the vertex (![]() ,
,
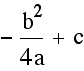 ) which
can be rewritten as (
) which
can be rewritten as (![]() ,
,
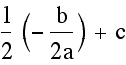 ). This leads us to the conclusion
that when b and c are being held constant the vertices of
). This leads us to the conclusion
that when b and c are being held constant the vertices of ![]() lie
on the line
lie
on the line 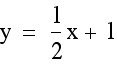 .
.