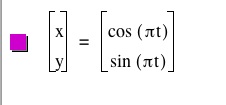
What is a parametric equation?
- parametric equations are just .another way to write functions to be graphed. When we have the continuous functions x = f(t) and y = g(t), they define ordered pairs (x,y). With parametric equations, the range of the graph that we can see, is determined by the range of 't' that we are using.

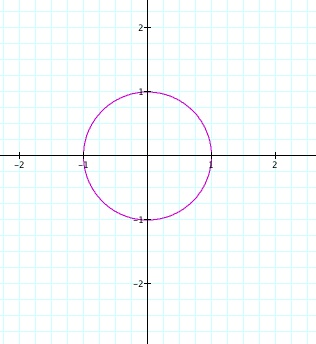
The following is a simple parametric equation of a circle. In order to make the circle the t value has to go from 0 to 2. If the value just goes to 1 then a semi-circle is made. As you can see from this then the radius is 1.

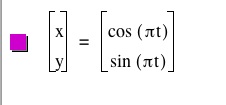
Let's explore more with parametric equations. If we change values you can see changes to the graph. In the first example we put coefficient in front of the cosine function and you can see the new shape that is formed.

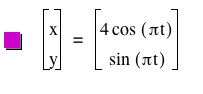
Now let's take a look and see what happens when a coefficient is added in front of the sine function.

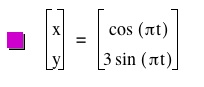
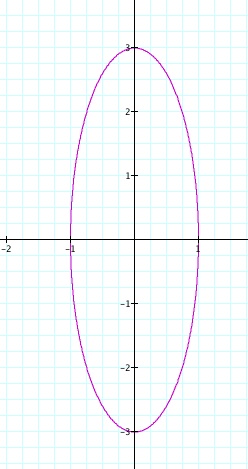
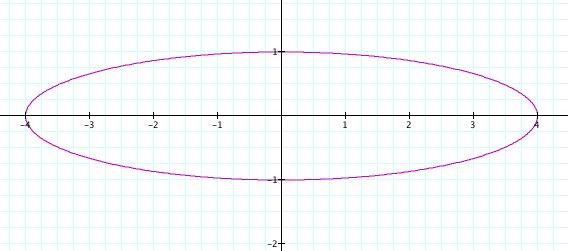
As you can see from the graphs one much wider and the other gets much higher. In the example fo the cosine function the coefficient was 4 and the width of the shape is eight, 4 units on either side of the origin. In the example of the sine function the coefficient is 3 so we and the height of the shape is 6, 3 units on top and 3 units on the bottom.

Now what happens when coefficients are added both in front of the cosine and sine function.

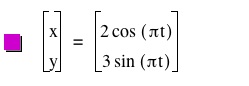
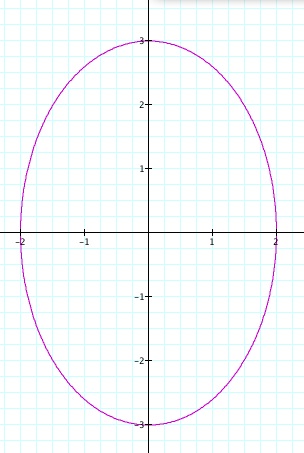
As you an see the graph sets both wider and higher. Through seeing what happens I would guess that if the coefficients in front of sine and cosine were the same you would again have a circle with the coefficient used being equal to the radius of the circle.

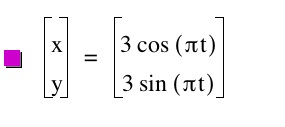
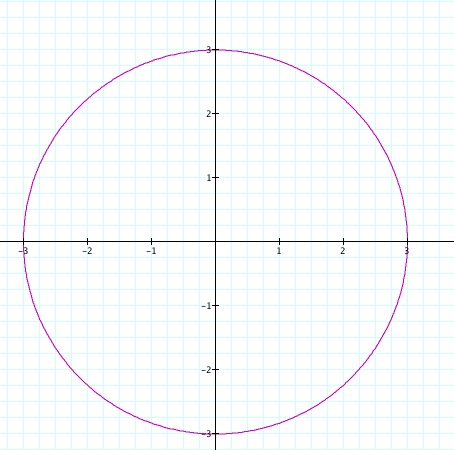
As you can see by this graph that a circle is formed that has a radius of 3. What you can also say about these graphs is that the coefficients represent the x and y intercepts of the ellipses and of the circles formed.