ASSIGNMENT 2

BRIAN DEITZ

#8)

In this assignment we are going to look at the following equation:

 

What will happen when values are plugged into this equation and a graph is formed? For example if d=0 wouldn't this graph cross the x-axis at -2 or would the parabola that is formed make an upward turn at -2. The other question that I asked myself is what will happen if a negative value was plugged into d (making this a positive d)? What I saw was graphs that did not change shape no matter what was plugged into the equation at d. These are the values I used for d in the equation and you can see the results below.

 

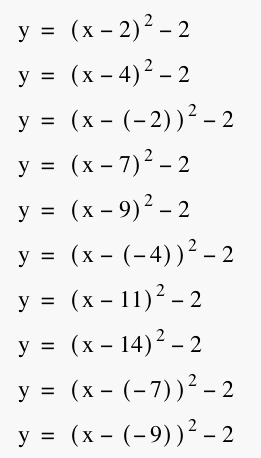
As you can see the shape of the parabolas stay the same no matter what value is plugged into d. The main thing that happens is that the minimum point of the parabola is equal to the d value that is plugged into the equation. Experimenting a little more the way to move the graph upward so the minimum point is on the x-axis is to remove the (-2) from the end of the equation. As you can see in the following graph the minimum point lies on the x-axis at one.

 

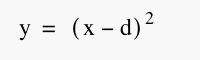
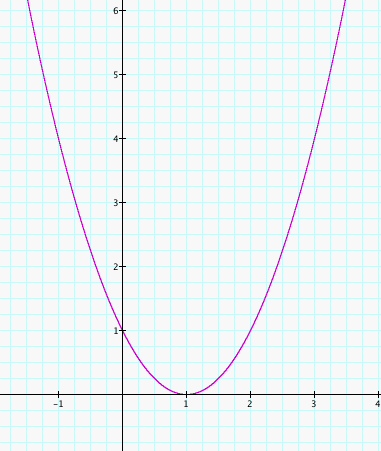
This exploration of the second degree equation allowed me to see what happens when numbers are added or subtracted to the equation. The curve only changes position on the graph in these cases.