

#1) In this assignment we are going to look at the centroids and orthocenters of triangles and ask ourselves what is the centroid of the triangle and how does it change as the triangle shape changes. We also are going to ask what is the orthocenter and how is the locatiom of the orthocenter different from the centroid.
THE CENTROID
The definition of a centroid of a triangle is the common intersection
of its medians (the lines joining each vertex with the midpoint
of the opposite side). So in essence the centroid divides each
of the medians into two equal parts.
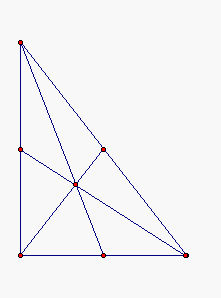
Looking at the centroid of a right triangle you can see that a median is a line segment that connects the vertex with the midpoint of the opposite side. This is more difficult to see in the next sketch with the triangle turned on its side. In the this second sketch you can also see that the centroid is also the center of gravity of the triangle.
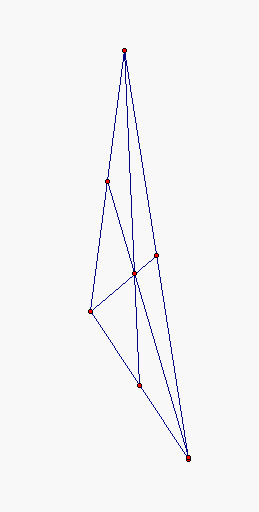
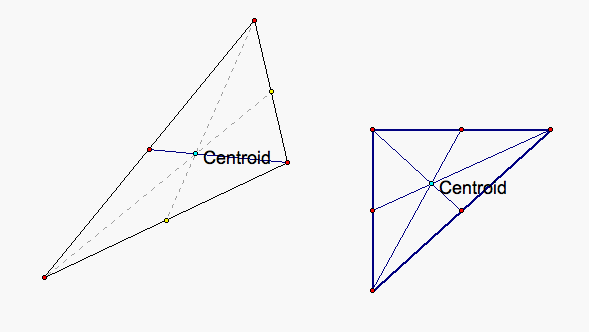
Here we see two more sketches that illuminate where the centroid sits on a regular triangle and again on a right triangle (on right). You can see in these sketches that the triangles are designed to "swirl" or spin around the centroid of the triangle so the centroid point stays the center of gravity of the figure.
THE ORTHOCENTER
To understand what the orthocenter
of a triangle is you first have to know what an altitude of a
triangle is in geometry. The altitude of a triangle is a straight
line through a vertex and perpendicular to (i.e. forming a right
angle with) the opposite side or an extension of the opposite
side. The three altitudes then intersect in a single point which
is called the orthocenter of the triangle.
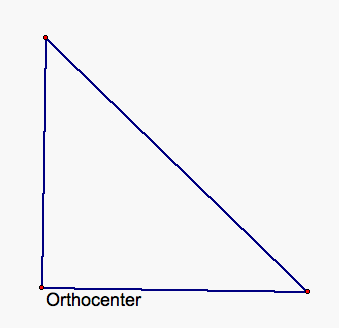
In the following sketch you can see that the orthocenter of the right triangle is on the vertex of the angle that forms the right angle. If you can imagine in your head you could see that the intersection of the altitudes (the orthocenter) is the polygon vertex of the right angle. In the next couple of sketches the altitudes are drawn for you.
In this second sketch you can see that the orthocenter has significantly changed location. Why does it sit where it does? The orthocenter sits where it does because that is where the altitudes meet in this acute triangle. For any acute triangle the orthocenter will be on the interior of the figure.
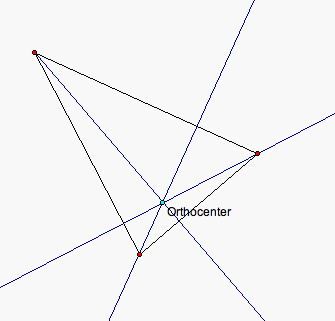
In this final sketch the orthocenter sits on the outside of the obtuse triangle. The reason this happens with this construction is because when the altitudes are drawn the intersection of these altitudes would be outside of the triangle. Therefore, the orthocenter moves completely out of the triangle where the altitudes meet. This always happens with a obtuse triangle.
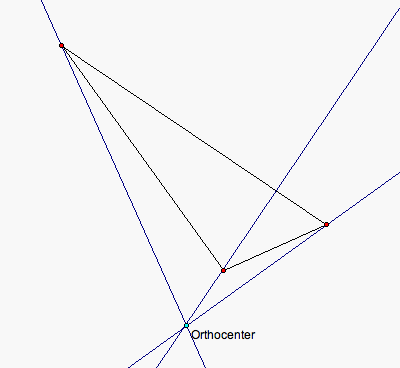
As you can see the orthocenter is definitely different than the centroid. Where the centroid is the center of gravity the orthocenter is just the location where the altitudes meet.