ASSIGNMENT 7

BRIAN DEITZ

 

# 7 LOOKING AT TANGENT CIRCLES

 

My first step was creating a script for the tangent circle.

GSP OF TANGENT CIRCLE.

Now let's explore what happens with tangent circles:

To create a tangent circle internal to a given circle these are the steps that I executed:

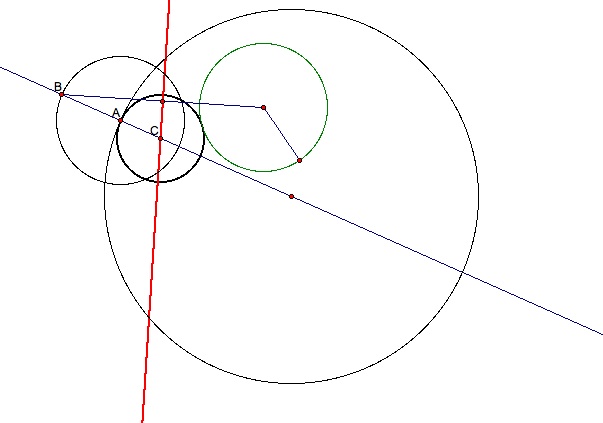
STEP 1 - Construct two circles with one that is inside the other. Then construct a line through an arbitrary point (we'll call point A) on the large circle and the center of the given circle.

STEP 2 - Construct a circle with the point A being the center and the radius equal to the radius of the smaller circle.

STEP 3 - Construct a point (we'll call point B) where the new circle intersects the line internal to the large given circle.

STEP 4 - Construct a line segment from the center of the small given circle to point B. Then take the midpoint of this segment and construct the perpendicular bisector of the segment.

STEP 5 - The point (we'll call point C) where the perpendicular bisector intersects the line drawn through point A is the center of the circle tangent to both circles where the smaller circle is external to the tangent circle.

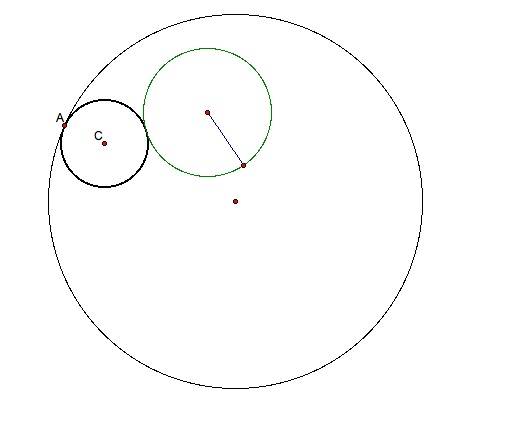
STEP 6 - Constructing the circle through point A with point C being the center gives you your tangent circle

This is what the construction looks like with all the construction lines present.

 

 

Here is the tangent circle without construction lines.

 

If there is a circle inside the other, like in the first picture, what is the locus of the center of the tangent

 

 

The red trace is the locus of the center of the blue tangent circle. As you can see the locus is an ellipse with foci at the center of the two original circles

 

What if the circles are dijoint like in the picture below? How many tangent circles willl there be?

Well, in this case there will be an infinite amount of tangent circles. To figure out one tangent circle, there has to be a given point on either of the circles that will be on the tangent circle also.

When the circles are disjoint the result is much different. The locus in this case turns out to be a hyperbola with the foci again the centers of the two given circle.