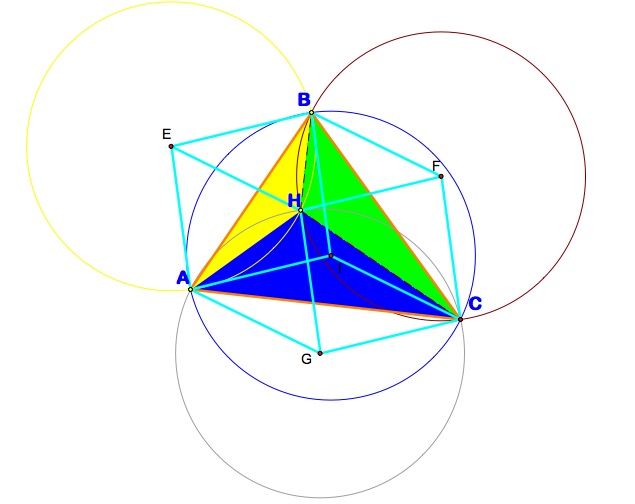
What is the orthocenter of the triangle?
- The orthocenter in the figure below can be created from the intersection of the altitudes of triangle ABC. The orthocenter will lie inside the triangle (and consequently the feet of the altitudes all fall on the triangle) under all conditionx except one. The following figure shows triangle ABC with orthocenter H. In this case with an acute triangle the point of concurrency will be on the altitudes.
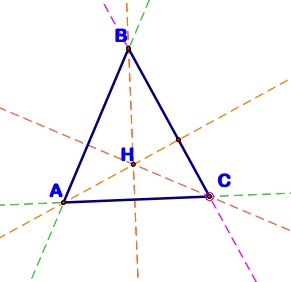
Notice that 3 additional triangles (called orthic triangles) were formed by constructing the orthocenter of triangle ABC. They are HAB, HAC and HBC
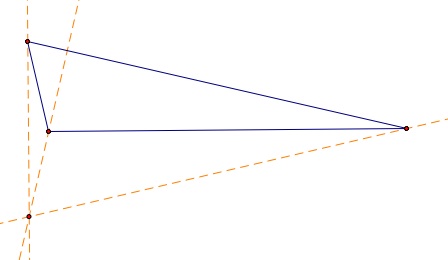
What is that one conditon where the orthocenter will not lie inside the triangle. Take a look at the following figure. This triangle is obtuse (one angle is greater than a right angle) and as you can notice the orthocenter lies on the outside.
What I did next was construct triangles between the orthocenter and the three vertices of the triangle. I then found where the orthocenters of the three smaller triangles would fall. As it turns out the orthocenters of the smaller triangles are the vertices of the original triangle.
I then constructed the circumcircles of the the four triangles involved (ABH, AHC, BHC and ABC). Circumcircles are a triangle's circumscribed circle that passes through each of the vertices. The center of this circle is called the circumcenter, and is the intersection point of perpendicular bisectors of the triangle.
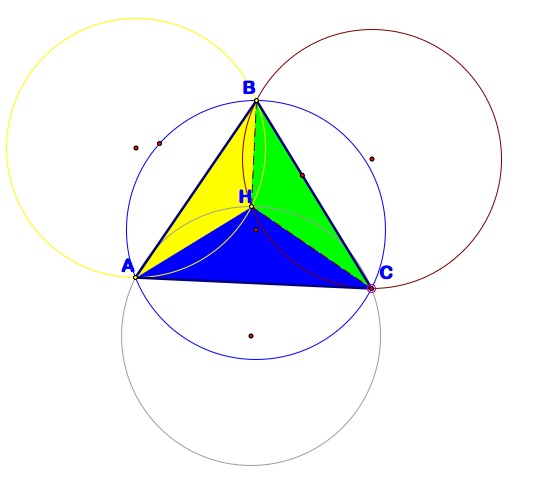
Here is a complete view of the circumcircles and altitudes.
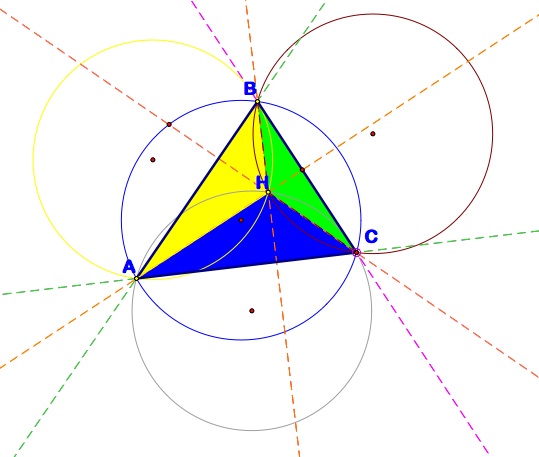
What can we say about all of this? This is some conjectures that I am came up with regarding altitudes of triangles, orthocenters and circumcircles.
- The radii of each circumcircle is exactly the same.
- All circumcircles will pass through the orthocenter (H) of the original triangle ABC.
- We know that the perpendicular bisector that intersects each side of the original triangle and travels through the orthocenter also intersects one of the centers of the outside circumcircles.
- A cube is formed by connecting the centers of the circumcircles with the orthocenter H (as seen here).