What is a pedal triangle?
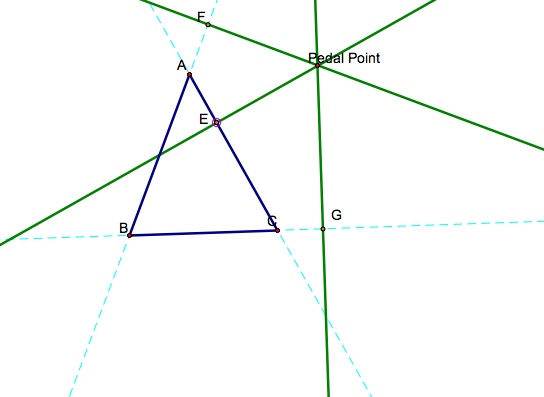
- A pedal triangle can be obtained by projecting a point onto the sides of a triangle. If you have a random point (Pedal point) on the outside of triangle ABC we can drop perpendiculars from the pedal point to the three sides of the triangle (these may need to be extended).

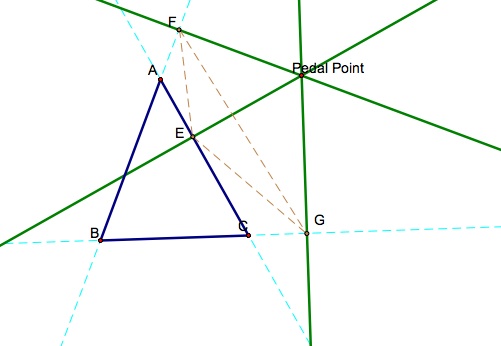
I then labeled the intersection points E,F,G from the pedal point to the sides AB, BC and CA. The pedal triangle then becomes EFG.
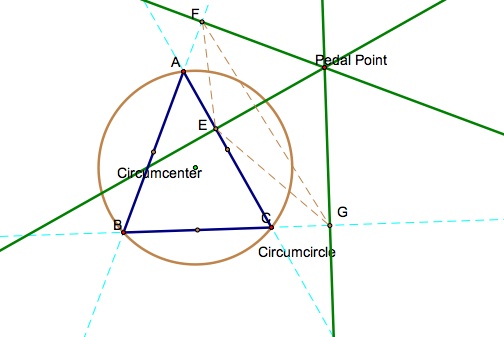
What if you were to draw in the circumcircle of triangle ABC. By definition, the circumcircle of triangle ABC passes through each vertex, and has the circumcenter as it's center.What relationship can be formed from this?
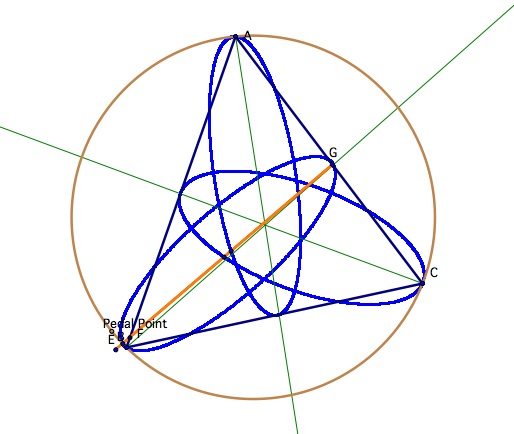
You will find from the following picture that when the pedal point lies on the circumcircle that the triangle disappears into a straight line. The orange line formed here is the pedal triangle that we took a look at earlier.
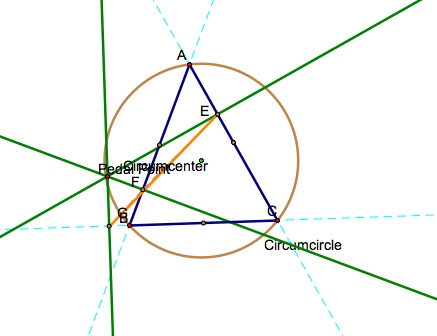
This is call the pedal line or Simson line. Here is a gsp of the Pedal triangle with the circumcircle. As you can see if the pedal point lies on the circumcircle you will ALWAYS have a Simson line and not a triangle
What are the conditions under which this happens?
When the pedal point moves fairly close in towards the sides of ABC, and it definitely occurs when the pedal point lands on any of its vertices.
Here is a demonstration of
this in which you can see what happens. Click here for the GSP file.
Looking at one last item dealing with pedal triangles. What can be formed from the paths that pedal triangles follow. If we were to mark the midpoints of the sides of triangle EFG and construct the circumcircle of triangle ABC merging the pedal point onto this circumcircle. By tracing the midpoints you can see the path in which these take around the pedal point. Just moving the pedal point or animating it you can see this in the next file. What is formed?