

The theorem states:
"The square on the hypotenuse of a right triangle is equal
to the sum of the squares on the two legs". You can also
find that the converse of this statement to also be true.
This theorem is talking about the area of the squares that are built on each side of the right triangle.
Accordingly, we obtain the following areas for the squares, where the green and blue squares are on the legs of the right triangle and the red square is on the hypotenuse.
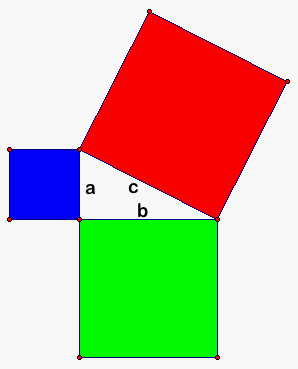
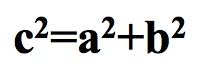
I. History
The Pythagorean theorem was a mathematical
fact that the Babylonians knew and used. This famous theorem is
named after the Greek mathematician and Philosopher, Pythagoras.
More than 4000 years ago, the Babyloneans and the Chinese already
knew that a triangle with the sides of 3, 4 and 5 must be a right
triangle. They used this knowledge to construct right angles.
By dividing a string into twelve equal pieces and then laying
it into a triangle so that one side is three, the second side
four and the last side five sections long, they could easily construct
a right angle. Before a proof was ever given, besides the Babylonians
it was thought that "Egyptian temple builders used ropes
in laying foundations, suggested that perhaps the obtained accurate
right angles by using marked ropes that could be stretched around
stakes to form a 3,4,5 right triangle."
A Greek scholar named Pythagoras, who lived
around 500 BC, was also fascinated by triangles with these special
side ratios. He studied them a bit closer and found that the two
shorter sides of the triangles squared and then added together,
equal exactly the square of the longest side. And he proved that
this doesn't only work for the special triangles, but for any
right triangle. The Pythagorean Theorem is Pythagoras' most famous
mathematical contribution. According to the legend, Pythagoras
was so happy when he discovered the theorem that he offered a
sacrifice of oxen. However 1000 years later, between the years
of 580-500 BC, Pythagoras of Samos was the first to prove the
theorem. It is possible that someone proved the theorem before
Pythagoras, but no proof has been found. Because of this, Pythagoras
is given credit for the first proof. Instead they wrote down everything
in words, for example: if you have a right triangle, the squares
of the two sides adjacent to the right angle will always be equal
to the square of the longest side.
We can't be sure if Pythagoras really was the
first person to have found this relationship between the sides
of right triangles, since no texts written by him were found.
In fact, we can't even prove the guy lived. Another Greek, Euclid,
wrote about the theorem about 200 years later in his book called
"Elements". There we also find the first known proof
for the theorem. Now there are about 600 different proofs.
Today the Pythagorean theorem plays an important
part in many fields of mathematics. For example, it is the basis
of Trigonometry, and in its arithmetic form it connects
Geometry and Algebra.
Plimpton 322, a Babylonian mathematical tablet dated back to 1900
B.C., contains a table of Pythagorean triples. The Chou-pei, an
ancient Chinese text, also provides the evidence that the Chinese
knew about the Pythagorean theorem many years before Pythagorean.
Pythagoras's theorem is unique for the peculiar way in which it has become a challenge to devise new proofs for it. These proofs are not necessarily any better; most rely on the same axioms but follow different paths to the result. Following the first proof, many proofs followed. Proofs have been found by Euclid, Socrates, and even President Garfield. The Pythagorean Proposition, by Elisha S. Loomis gives 367 ways to prove this popular theorem.
A little info on a man named Pythagoras
Pythagoras' father Mnesarchus wanted to made sure that his son would get the best possible education. His first teacher was Pherecydes and Pythagoras stayed in touch with him until Pherecydes' death. One of the teachers of Pythogoras, Thales of Miletus, recommended that he go to Egypt to study so around 547 BC when he was 23 years old he went to Egypt. He stayed in Egypt for 21 years learning a variety of things including geometry from Egyptian priests . It was probably in Egypt where he learned the theorem that is now called by his name. He later moved to Croton in the south of Italy where he started a school which concentrated in the teaching and learning of Mathematics, Music, Philosophy, and Astronomy and their relationship with Religion.
Now let's talk a bit about the theorem that bears his name. The Egyptians knew that a triangle with sides 3, 4, and 5 make a 90 degrees angle. The Egyptians used a rope with 12 evenly spaced knots that they used to build perfect corners in their buildings and pyramids. So why is it called the Pythagorean Theorem? Even though the theorem was known long before his time, Pythagoras certainly generalized it and made it popular. It was Pythagoras who is attributed with its first geometrical demonstration.
The key to this proof of the Pythagorean Theroem is the area of trapezoid. This proof with a trapezoid was discovered by James Garfield in 1876 when Garfield was having a mathematics discussion with members of Congress five years prior to becoming the 20th President of the United States. He divided the trapezoid into three triangles and found the area of the trapezoid and then the sum of the areas of the triangles.
This proof was derived from the oldest existing Chinese texts containing formal mathematical theories that were produced during the Han period. The Arithmetic Classic of the Gnomon and the Circular Paths of Heaven (Chou Pei Suan Ching) is dated before the 3rd century B.C and contains various modern mathematical principles such as working with fractions using a common denominator, and proofs of many geometrical theories. The text contains an accurate process of division for finding out the square root of numbers.
In fact, the Chou Pei presents the oldest known proof of the right-angle triangle theory in the hsuan-thu diagram. This theory, commony known as the "Pythagorean theorem," shows that the sum of the squares of the legs of a right triangle is equal to the squares of the hypotenuse.
The Chou Pei was not an isolated academic text shared only by a few ancient Chinese mathematicians. The principles in the text were reflected in the popular approach known as chi-chu, or "the piling up of squares" which was a process of using geometry to solve algebric problems.
In many ways, Bhaskara represents the peak of mathematical and astronomical knowledge in the 12th century. He reached an understanding of calculus, astronomy, the number systems, and solving equations, which were not to be achieved anywhere else in the world for several centuries or more. Bhaskara (11141185, India) was one of the first mathematicians to gain a thorough understanding of number systems and how to solve equations, several centuries before European mathematicians. He wrote six books on mathematics and astronomy, and led the astronomical observatory at Ujjain.
Euclid was a very influential and important figure in mathematics when he arrived on the mathematical scene around 300 B.C. He began his first documented studies, it appears, at the Academy from the followers of Plato. He was then drawn to study at Alexandria where the new, great Alexandrian Library was established by Alexander the Great. Euclid's main goal at Alexandria was to set up a school of mathematics. However, what brought Euclid to fame forever in the mathematical world was his writing of the Elements. Euclid's Elements has been studied for century upon century and is still studied today. This work consists of 13 books with 465 propositions from plane and solid geometry as well as number theory. There are very few theorems in the Elements that are of Euclid's own design but the way that he proved and organized these theorems is what has given him such a revered place in the history of mathematics.
Euclid started with the plain basics- these were 23 definitions, 5 postulates, and 5 common notions or general axioms. From this point Euclid could prove his first theorem. Using the basics plus the first proved theorem he could go on and prove the second theorem and so forth. This systematic and almost flawless way to prove each consecutive theorem was beautiful, a logical work of art. This approach was so significant because it follows a framework in which we start with a few givens and then build upon these, each new theorem building on the previous ones until all that is needed is proved. This axiomatic approach is still widely used today, over 23 centuries later. To put the significance of the Elements into perspective, the Elements has appeared in over 2000 editions.
http://www.arcytech.org/java/pythagoras/history.html
http://www.saxakali.com/COLOR_ASP/developcm3.htm
http://www.cut-the-knot.org/pythagoras/index.shtml
http://www.gvsu.edu/math/students/st/Euclid.htm
http://jwilson.coe.uga.edu/EMT668/emt668.student.folders/HeadAngela/essay1/Pythagorean.html