Disclaimer: I have never worked with parametric equations before.

We're going to take this investigation slow starting with something basic.

Let's explore a little with cos(at) and sin(bt). Nothing exciting happens when a and b are equal, you get the same unit circle. Also, I have set the range of t to be 0 to 100.

But check out what happens when a=2 and b=3...

Let's go on ahead and keep a=2 and vary b...

b=4

b=5

b=6

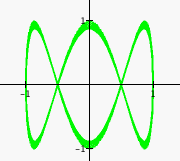
I think we are seeing a pattern here. When b is even, the graph is closed. When b is odd, the graph is missing a "half." For example, when b=5, the graph is the graph of b=4 plus half of another pattern.

One quick note. Changing the range of t from 1000 to 500 to 100 to 10 results in the thinner graph on the right.

Now let's see what happens when we leave b constant and vary a. (t = 10 and 1000)

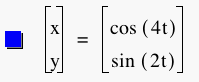
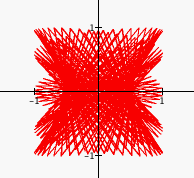
So, the graphs are different depending on whether you vary a or b. This makes sense since a and b correspond to different funcions, sine and cosine. Also, when you vary a, which corresponds to the cosine function, all the graphs are different from each other, whereas when you vary b, corresponding to the sine function, all the graphs take on the same shape.