Let's dissect this thing! Let a, b, and k be real numbers, b and k not equal to 0. Let's first recall what cos(), where a=0, b=1, and k=1, looks like.

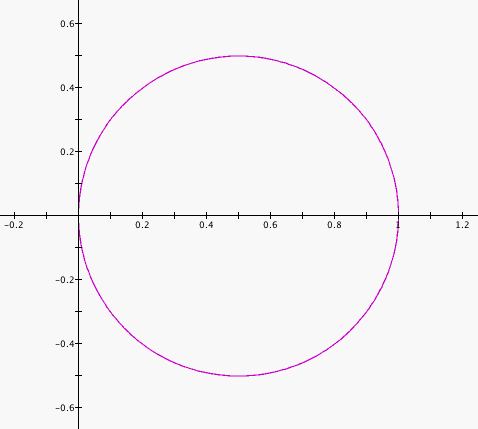
Not very interesting. Now let's leave b=1, change k to 2, and vary a.

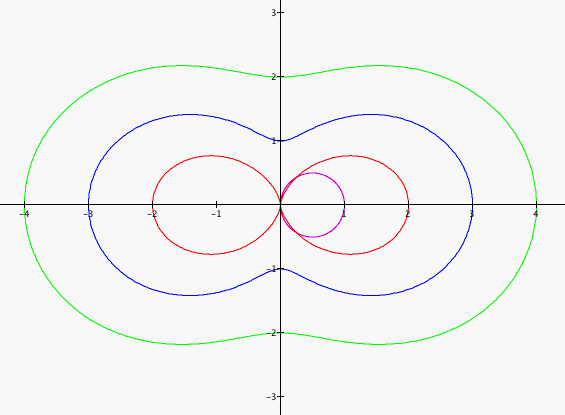
A couple of things have happened. First, by assigning a the value of 1, the graph starts to separate into two closed shapes, but then begins to open up again as the value of a increases. Or maybe as the value of a changes from the value of b, which in the case of these graphs remains equal to 1.

Let's continue to leave b the same, vary a, and this time change k to 3.

OK, now there are 3 closed, petal-like shapes and with each change in a, the shapes become larger. So, the value of k seems to coincide with the number of "petals." Also, looking back at the first graph and comparing it with this one, the only time the graphs are closed is when a and b both equal 1. In the blue and green graphs, the values of a and b are not equal and consequently the graphs are not closed. Why?

Let's try a few more values of k, say 4, 5, and 6, this time however let's make a and b equal.

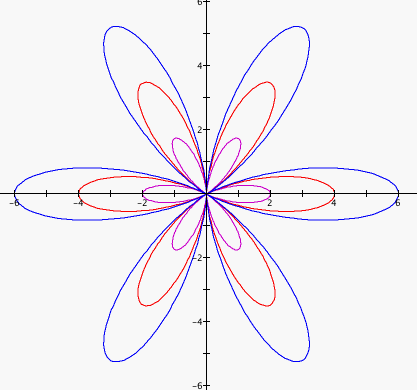
As I thought, the graphs are all closed when the values of a and b are equal! So, the values of a and b are essentially scalars. The larger a and b are, the larger the petals are.

If the values of a and b are just scalars, let's see what happens with r = bcos().

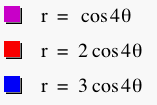
That's pretty interesting. It certainly didn't do what I thought it was going to do. I thought it would look exactly like the graphs above. The graphs are still scaled by the value of b, but for some reason the graphs, where is multiplied b an even number, have two times the number of petals as the even number. I tried 4, 5, and 6 above and this didn't happen, so I am going to assume that not having an a value is affecting the number of petals.

Have you ever wondered what would happen if you replaced cosine with sine?

Notice anything yet? They're so pretty let's do one more, just to make sure my eyes do not deceive me.

I hope you have finally noticed the difference when you replace cosine with sine. The sine graph is rotated by 90 degrees. So looking at the five petal flower, one of the petals lies on the x-axis when using cosine and on the y-axis when using sine. This should be expected if you think about when sine and cosine equal one.