
Stephani Eckelkamp
Parametric Equations: What does it all mean
Let us begin by defining parameter.
paŠramŠeŠter
(parametric adj.)
1.
Mathematics definition.
1. A constant in an
equation that varies in other equations of the same general form, especially
such a constant in the equation of a curve or surface that can be varied to
represent a family of curves or surfaces.
2. One of a set of
independent variables that express the coordinates of a point.
~~
Now that we know what it means, we can explore parametric equation and
their graphs ~~
Parametric equations in the plane is a pair of functions
x = f(t) and y = g(t)
which describe the x and y coordinates of the
graph of some curve in the plane.
A very basic parametric equation is
x = cos (t)
y = sin (t)
this can also be written as
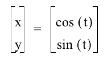
Explorations
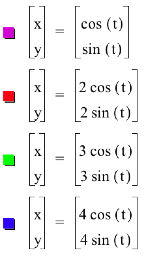
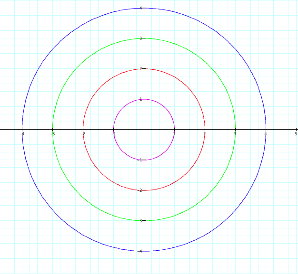
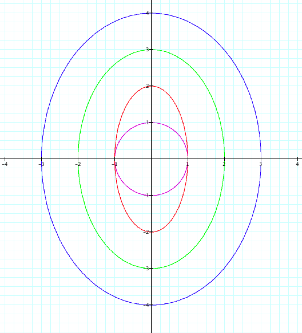
By increasing the coefficient of the x coordinate
function and the y coordinate function we are able to see where the graphs
cross the x and y axis respectively.
What happens if the x and y coefficient of
these coordinate functions differ?
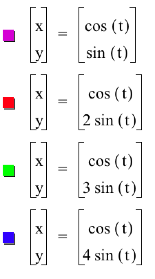
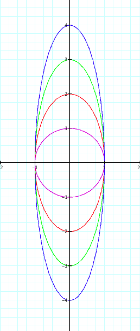
The coefficient attached to the x coordinate
function is where the graph will cross the x axis, and the y coordinate
function will cross the y axis.
We can see this in both the above and below
examples.
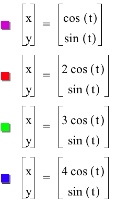
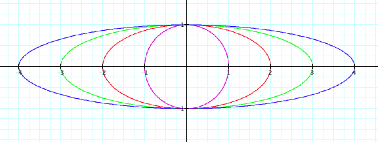
Further explorations:
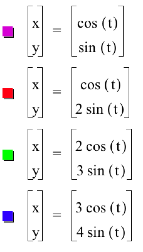
What do you think will happen when a number
is attached to t?

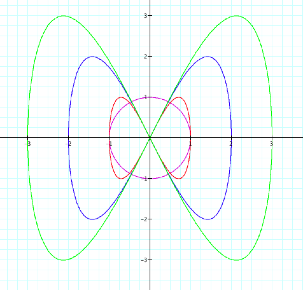
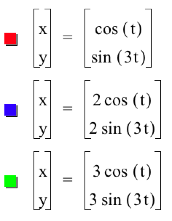
By multiplying t by 2 the graph folds over
itself in one place. What do you
think will happen for 3?
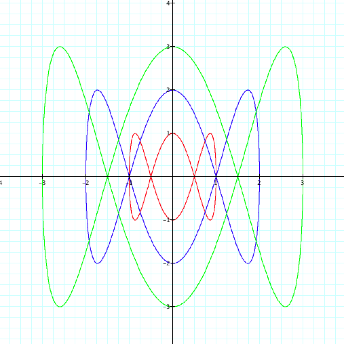
Click here to see an animation for this
parametric equation with the slider values from 1 to 10.
What do you notice about how many times the
graph crosses itself in relation to the n value given? Does the coefficient of the x and y
coordinate ideas that you previous had hold true in these cases? Spend some time working with the
link below, to see if your conjectures hold true for multiple cases.
For further explorations open this copy of graphing calculator
You can also graph these equations using a
graphing calculator (ie TI series).