Stephani Eckelkamp

ÒGraphing Fun with CalculusÓ

Optimization is an idea that most students in Calculus classes become very familiar with!  Here is an exploration of optimization using GSP and Excel to help give a visual representation for exactly what optimization looks like.

 

For this investigation I will be looking at the following problem: 

Explore problems of maximization such as the lidless box formed from a 5Ó x 8Ó sheet with a square removed from each corner.

 

A good place to start is by constructing a model in GSP.

Here is the one I came up with

 

 

Rectangle ABCD is the 5Óx  8Ó piece of paper I started with.  The squares cut out are hÓ x h.Ó

l is the length and w is the width of the lidless box formed when hÓ x hÓ squares are cut out.

 

Question:

What h will maximize the volume of the lidless box?

Make a guessÉwhat do you think it is?

 

Click this GSP link to manipulate.

**Note the chart in the top right corner**

 

What does the chart represent?  What formula is l x w x h ?

 

What do you think the graph of the volumes in relation to the height will look like?  Why?

 

Here is a picture of the graph done in GSP

Link to GSP graph and spreadsheet

 

 

Here is the graph done in excel

Link to excel graph and spreadsheet

 

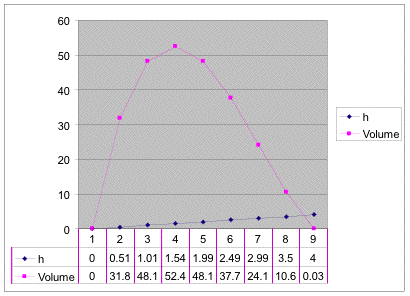
For this problem the maximum h is approximately 1.5.

 

Notice in both graphs that the start and end at 0.  Why is this true for this problem?  How does this relate to closed intervals?  What are the closed intervals for this problem?

Another exploration

 

Question:

A rectangle is enclosed in a parabola with the equation f(x) = 4 - x2 .

The vertices of the rectangle are (-x,0), (-x,y), (x,0), and (x,y).

 

Here is a picture of the sketch of this graph

 

 

Click here to open the GSP file to manipulate this graph

**Note the table to at the top right

 

What do you think the area graphed will look like?

 

Here is the graph in excel

 

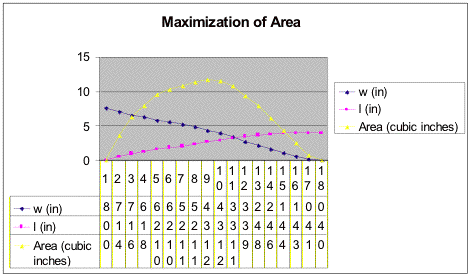
What might the graph look like in relation to the length and the width of the rectangle?

Here are both of them graphed on the same plane.

 

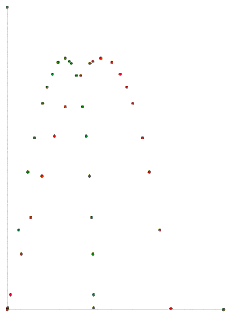
Which color goes with width and length?  Hint:  Look back at the original graph.

Explain why one graph has a greater domain than the other.

 

Here is the chart used for these graphs

 

w (in)

l (in)

Area

7.59

0.01

0.06

7.07

0.52

3.69

6.6

0.96

6.37

6.26

1.27

7.96

5.82

1.64

9.55

5.54

1.86

10.32

5.25

2.08

10.91

4.85

2.36

11.45

4.33

2.69

11.66

3.98

2.89

11.52

3.4

3.19

10.86

2.69

3.49

9.4

2.19

3.66

8.03

1.62

3.81

6.19

1.09

3.91

4.27

0.65

3.97

2.58

0.17

3.99

0.68

0.02

3.99

0.09

 

The maximum for this problem is between 4 and 4.8.

 

Choose an optimization word problem, create a picture in GSP and graph to find an approximation of the maximum.

Return