Stephani Eckelkamp

 

Medial Triangles

 

 

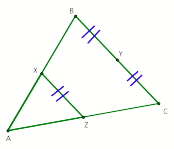
Medial triangles are formed by connecting the midpoints of any one triangle (as seen below).

 

 

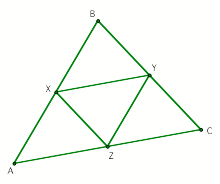
Points x, y, and z are the midpoints of their respective sides of , therefore  IS THE MEDIAL TRIANGLE.

 

~~~NOW THAT WE KNOW WHAT IT LOOKS LIKE LET US LOOK AT SOME SPECIAL PROPERTIES OF MEDIAL TRIANGLES~~~

 

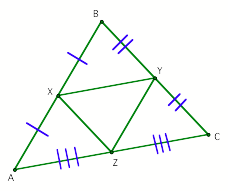WHAT DO WE ALREADY KNOWÉ

 

 

 

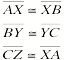            WE KNOW THESE SEGMENTS ARE CONGRUENT BECAUSE THE MIDPOINTS

CUT THE SEGEMTNS IN TO TWO EQUAL PARTS.            

 

 

 

Theorem:  If a line segment joins the midpoints of two sides of a triangle,

Then it is parallel to the third side and equal to one-half of it.

 


After applying the theorem above we get:

 

 

 

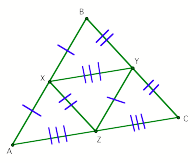
Can we demonstrate this?  LetÕs look at it in the coordinate plane.

 

 

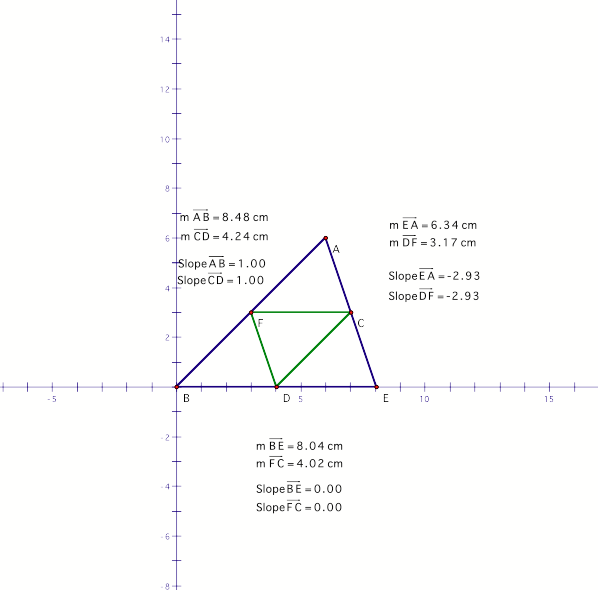
As we can see above, the measure of the blue triangle sides is

two times larger than the parallel side formed by the medial triangle. 

We know that the sides formed by the medial triangles are parallel because their slopes are equal.

To view this picture in GSP click here

 

 

Can we use the medial triangle theorem to show that the area of the medial triangle is ¼ the area of the original triangle?

Set up a two column proof to see if you can reason this.  HINT:  your given will be some part of the medial triangle theorem.

 

After you have tried to work out a proof click here for guidance or to check your answer.

 

COMPARING THE MEDIAL TRAINGLE TO THE TRIANGLE CENTERS

 

What are the triangle centers?

 

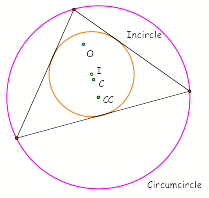O is the orthocenter, which is created by the intersection of the three altitudes of the triangle.

 

I is the incenter, which is the point that is equidistant from the tree sides of the triangle.

 

CC is the circumcenter, which is formed from the perpendicular bisectors.  The point is equidistant from the three verticies.

 

C is the centroid, which is the common intersection of the three medians of the triangle. 

 

 

 

 

 

 

Triangle centers in comparison to the medial triangle

 

What are the three types of triangles?  Where do you think the centers might be in each of these cases?

 

 

AcUTE TRIANGLE

 

 

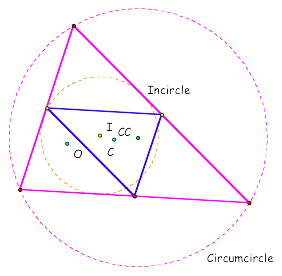
Notice that most of the centers are located inside the medial triangle.  Why isnÕt the orthocenter inside the triangle?

  Do you think that it will ever be located inside the medial triangle? 

 

RIGHT TRIANGLE

 


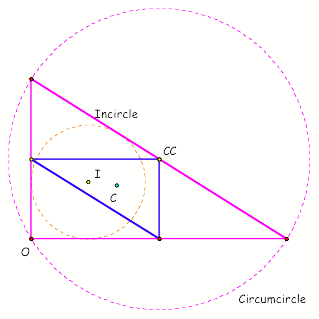
What do you notice about where the orthocenter and the circumcenter are located?

The orthocenter is located on the vertex of the right angle of the original triangle, and the circumcenter is located on the vertex of the right angle of the medial triangle.

 

Does the centroid look like it is the center of the medial triangle?  LetÕs test this in GSP.

 

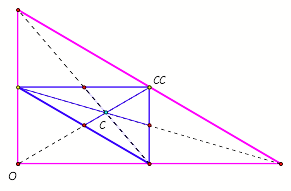
We can see the centroid is the intersection of the medians of the medial triangle and the original triangle.

Can you thin of possible reasons why this is true?

Write down some ideas in this word document and print it out.

Cut and paste this picture into your file.

Also create either an obtuse or acute triangle to add your word document.  Use this link to create your pictures.

 

What do you think will happen to the orthocenter and the circumcenter in an obtuse triangle?

 

 

OBTUSE TRAINGLE

 

 

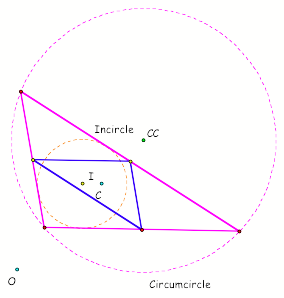
Did the orthocenter and the circumcenter move where you thought they would?

  Explain your reasoning in your word document.

 

Looking at the centers of circles is there anything you can deduce after seeing how the centers relate

to one another when the triangle changes from acute, right, and obtuse?

 

For a hint click here

 

Check to see if your prediction is true in this GSP file

 

Return to homepage