Stephani Eckelkamp

The Pedal Point as the Orthocenter

Question: Are there any special properties of the pedal triangle when the pedal point is located on the orthocenter?

Exploration:

First let us begin with a picture when the pedal point falls on the orthocenter.

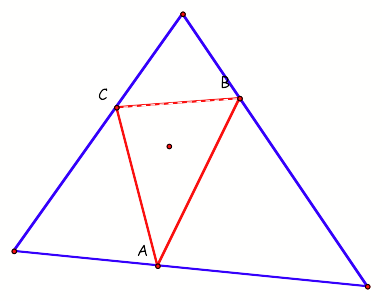
For our first exploration we will only focus on the original triangle being acute.

Working with this GSP file, see if you can find any special properties on the pedal triangle.

Try using the script tools to see if any special properties can be seen. (If you do find something, make sure that you can move the triangle to make sure the property holds true for different movements of the construction (only working with acute triangles).

Did you find anything interesting?

Try creating a perpendicular line from the pedal triangle point and the side it lies on.

Here is an example.

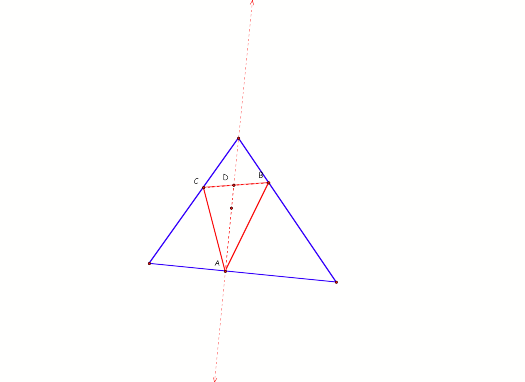
Line AD is the perpendicular line created from highlighting A and the side of the original triangle it is located on.

Do this for all of the angles.

Your picture should look something like this.

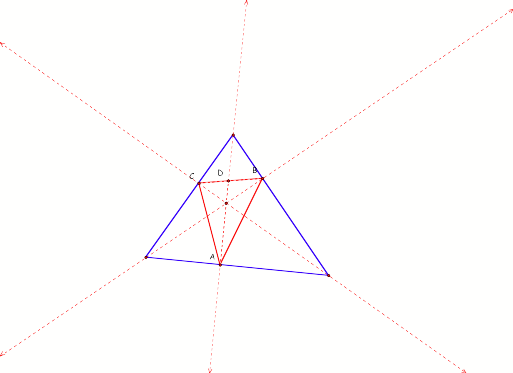
While keeping your original triangle acute, see if you can find any special properties of the pedal triangle. Explore segments, angles, area, and anything else that you think might have a relationship of interest.

Here is one relationship that I found interesting.

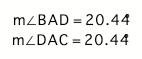
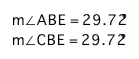
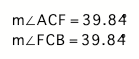
From the above measurements we can see that from our construction the perpendicular lines are angle bisectors of the pedal triangle.

Move the triangle around to see if our construction supports this idea.

Click here to move construction.

Did you notice anything different about the measurements when the triangle was obtuse? How about when it was a right triangle?

Here is a picture when the original triangle is right.

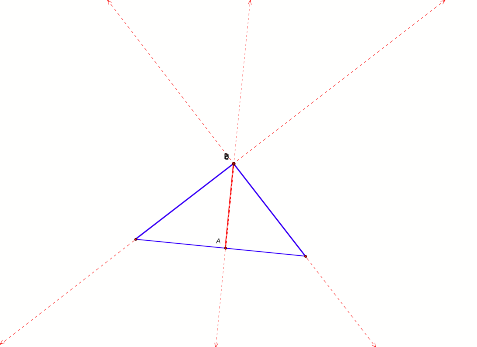
What is segment AB forming in our original triangle? Is angle B still being bisected?

Can you create the altitude for the other two sides? Click here to work with this file.

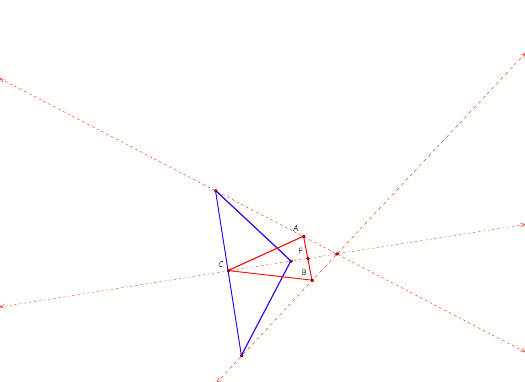
What if the original triangle is obtuse?

Here is a picture:

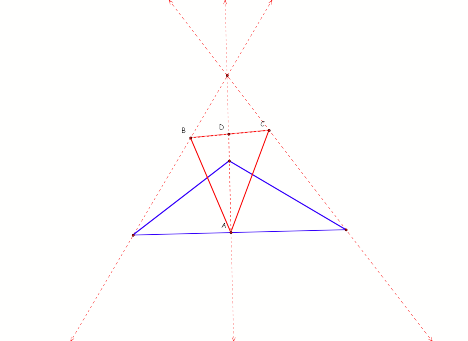
Here we can see some things changed. The pedal triangle is no longer enclosed in the original triangle, only one angles is being bisected by a perpendicular line, and the orthocenter is not located in either of our triangles.

Explore the pedal triangle when the original triangle is obtuse.

What do you notice about any angles being bisected? Is it possible for more than one angle to be bisected when the original triangle is obtuse? Why or why not?

Here is another picture:

Further Explorations:

What if the pedal point is on the incenter?

Circumcenter?

Center of the 9 point circle?

Centroid?

Side of the original triangle?

Blank GSP file with scripts tools to further explore the above mentioned extensions