Sarah Hofmann
EMAT 6680
Summer 2006
Assignment
11
For
assignment 11, we have chosen to write up problem number 2 because in
our opinion it produced the most interesting and beautiful graphs.
To begin we
need to investigate the equation
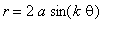 for
varrying a and k. We begin by fixing a = 1 and varrying k through
the non-zero integers -3..3from least to greatest.
for
varrying a and k. We begin by fixing a = 1 and varrying k through
the non-zero integers -3..3from least to greatest.
![[Maple Plot]](images11/assign1112.gif)
![[Maple Plot]](images11/assign1113.gif)
![[Maple Plot]](images11/assign1114.gif)
![[Maple Plot]](images11/assign1115.gif)
![[Maple Plot]](images11/assign1116.gif)
![[Maple Plot]](images11/assign1117.gif)
We can
conclude that the difference between a positive and a negative value
for k is a rotation about the x-axis. This is consistant with
sin(t) being an odd function. It also appears that the value of k
dictates how many "leaves" the function will have. If k is odd,
the function will have k leaves. If k is even, the function will
have 2k leaves. The leaves all seem to start at the origin,
tangent to the x-axis in the first quadrant. Let's test our
hypothesis with a few large values of k, say 5 and 16.
![[Maple Plot]](images11/assign1118.gif)
![[Maple Plot]](images11/assign1119.gif)
Indeed, the
above graphs have 5 and 2(16) = 32 leaves and they are tangent to the
x-axis as believed.
Let us
continue our investigation of the equation
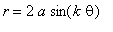 by
fixing k = 5 and varrying a through the non-zero integers from -3..3,
beginning with the smallest integer and working up.
by
fixing k = 5 and varrying a through the non-zero integers from -3..3,
beginning with the smallest integer and working up.
![[Maple Plot]](images11/assign11111.gif)
![[Maple Plot]](images11/assign11112.gif)
![[Maple Plot]](images11/assign11113.gif)
![[Maple Plot]](images11/assign11114.gif)
![[Maple Plot]](images11/assign11115.gif)
![[Maple Plot]](images11/assign11116.gif)
We can draw
two conclusions from the above graphs. We first conclude that the
difference between a and -a is a rotation about the x-axis. This
is consistant with our knowledge of flipping regular functions about
the x-axis by multiplying by a negative. Second, we must be
areful to pay attention to the scale of the above graphs. It
seems that the radius of the leaves is equal to |2a|. Lets check
our hypothesis with a larger number for a, say a = 22.
![[Maple Plot]](images11/assign11117.gif)
Success!
The petal has a radius of 44, as we suspected.
We must now
investigate the equation
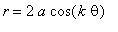 for
various values of k and a. We will begin as above by fixing a =
1and varrying k from -3..3
for
various values of k and a. We will begin as above by fixing a =
1and varrying k from -3..3
![[Maple Plot]](images11/assign11119.gif)
![[Maple Plot]](images11/assign11120.gif)
![[Maple Plot]](images11/assign11121.gif)
![[Maple Plot]](images11/assign11122.gif)
![[Maple Plot]](images11/assign11123.gif)
![[Maple Plot]](images11/assign11124.gif)
Here we had
some expected and unexpected results. It seems that again, if k
is even, the graph has 2k leaves and if k is odd the graph has k
leaves. Since cosine is an even function, we expected no
difference between the graphs for positive values of k and negative
values of k, which did occur. However here, the graphs seem to be
"centered" about the positive x-axis instead of tangent to it.
This makes sense, since sin(0) = 0 and cos(0) = 1.
We now
explore various non-zero values of a from -3..3 as we did with the sine
version, we will fix h = 5 again.
![[Maple Plot]](images11/assign11125.gif)
![[Maple Plot]](images11/assign11126.gif)
![[Maple Plot]](images11/assign11127.gif)
![[Maple Plot]](images11/assign11128.gif)
![[Maple Plot]](images11/assign11129.gif)
![[Maple Plot]](images11/assign11130.gif)
The results
for varrying a seem to be the same as the sine version of the equation.
A negative value of a rotates the graph about the y-axis and the
length of a leaf is |2a|.
Let us
continue our investigations by adding another variable to the function.
We will now consider the function
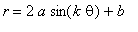 for
various values of a, k and b. We already know how a and k affect
the graph. So lets fix a = 2, k = 3, and vary through the
integers 1..5.
for
various values of a, k and b. We already know how a and k affect
the graph. So lets fix a = 2, k = 3, and vary through the
integers 1..5.
![[Maple Plot]](images11/assign11132.gif)
![[Maple Plot]](images11/assign11133.gif)
![[Maple Plot]](images11/assign11134.gif)
![[Maple Plot]](images11/assign11135.gif)
![[Maple Plot]](images11/assign11136.gif)
That was
definately unexpected! Something interesting seems to be
happening around b = 4. Lets examine it further by looking at
values close to 4, say b = 3.25, b=3.5, b=3.75, b=4, b=4.25, b=4.5, and
b=4.75
![[Maple Plot]](images11/assign11137.gif)
![[Maple Plot]](images11/assign11138.gif)
![[Maple Plot]](images11/assign11139.gif)
![[Maple Plot]](images11/assign11140.gif)
![[Maple Plot]](images11/assign11141.gif)
![[Maple Plot]](images11/assign11142.gif)
![[Maple Plot]](images11/assign11143.gif)
Indeed, it
seems that the "double" graph gets smaller and smaller as b approaches
4 from the left until the graph is normal at 4, then the graph begins
breaking apart at the origin as the value of b moves away from 4 to the
right. We can see this and the fact that the double graph appears
at b = 0 from the animation below.
The next
question to answer is, why 4? Why not some other number? We
hypothesis that this is because 4 = 2*2=2a. Let's check our
hypothesis with a different value of a, say a = 5, k = 3, and b = 8..12.
![[Maple Plot]](images11/assign11144.gif)
![[Maple Plot]](images11/assign11145.gif)
![[Maple Plot]](images11/assign11146.gif)
![[Maple Plot]](images11/assign11147.gif)
![[Maple Plot]](images11/assign11148.gif)
Success!
Our hypothesis seems to hold.
We are now
to repeat our investigation with the equation
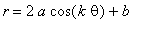 and
we expect our results to be exactly the same. We will verify this
by checking the equation for a = 2, k = 3, and b = 3.25..4.75 ranging
over the quarter values.
and
we expect our results to be exactly the same. We will verify this
by checking the equation for a = 2, k = 3, and b = 3.25..4.75 ranging
over the quarter values.
![[Maple Plot]](images11/assign11150.gif)
![[Maple Plot]](images11/assign11151.gif)
![[Maple Plot]](images11/assign11152.gif)
![[Maple Plot]](images11/assign11153.gif)
![[Maple Plot]](images11/assign11154.gif)
![[Maple Plot]](images11/assign11155.gif)
![[Maple Plot]](images11/assign11156.gif)
Since our
results are as we expected, we now check for values of a = 5, k = 3,
and integers b = 8..12
![[Maple Plot]](images11/assign11157.gif)
![[Maple Plot]](images11/assign11158.gif)
![[Maple Plot]](images11/assign11159.gif)
![[Maple Plot]](images11/assign11160.gif)
![[Maple Plot]](images11/assign11161.gif)
Our results are as we hypothesized. You can click here
for an animation showing a similar
phenomenon as seen for the sine
equation.
We conclude
our exploration with an investigation of the equation
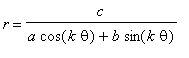 . We will
proceed by fixing three of the variables (a,b,c, and k) and varying the
fourth.
. We will
proceed by fixing three of the variables (a,b,c, and k) and varying the
fourth.
We will begin by fixing, a = b = c = 1, and exploring
k. Learning from our previous experience, we will begin by
looking at k = 4, -4, 5, and -5 to see if we can recognize any vertical
or horizontal flips by changing k from positive to negative.
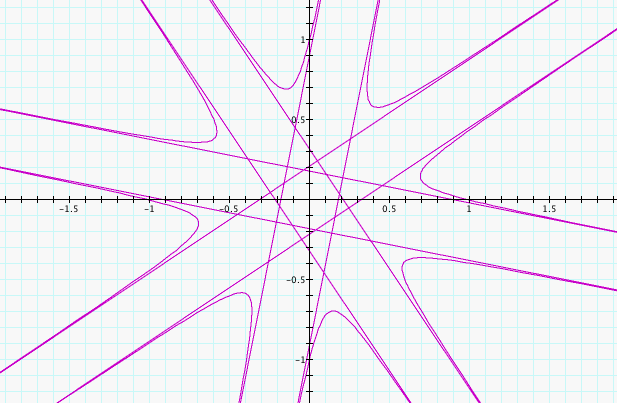
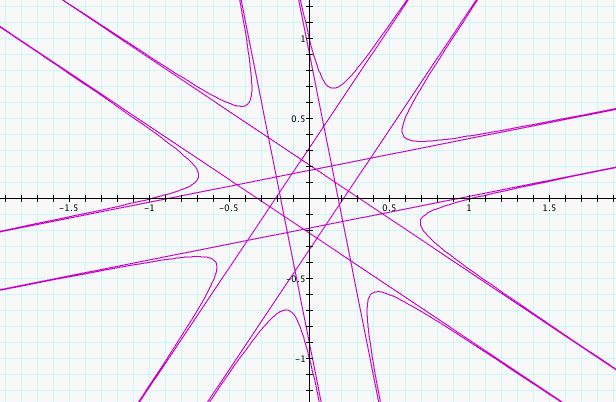
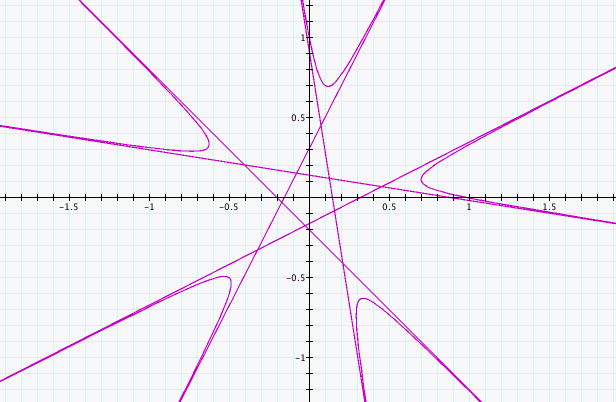
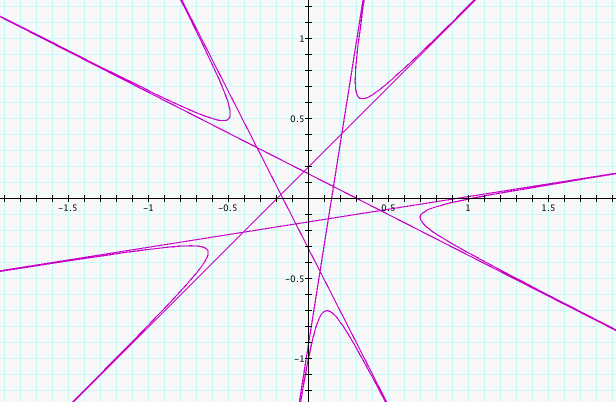
We can
immediately see that changing k = 4 to k = -4 and k = 5 to k = -5 flips
the graph about the x-axis. This is consistant with our knowledge
of the fact that sin starts increasing and cosine starts decreasing
when moving positively away from 0, however both sine and cosine are
decreasing when moving negatively away from zero, so the picture would
be shifted counter-clockwise by a positive k value and clockwise by a
negative k value.
In evaluating the above pictures, it also seems that k has similar
effects on this equation that it had on our previous equations.
It seems that when k is an odd integer, there is a k point star in the
middle, but when k is an even integer there is a 2k point star in the
middle. Let's explore this phenomenon and see what happens when k
is not an integer via the animation below.
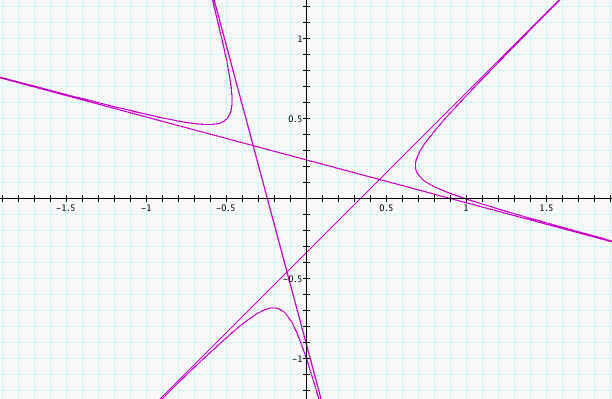
We can observe a few different
things when watching the animation. First, our assumption about
the number of points of the star as k varries is correct for non-zero
and non-unit values of k. Second, we can see that when k is not
between -1 and 1, as k varries, the graph seems to spin and create new
stars on the odd integers that double immediately after the odd
integers. Finally we notice that there is a fixed point of (1,0)
for all of the graphs. We also notice that the stars completely
fall apart when the value of k is between -1 and 1. Probably
because the functions 1/(sin(x)) and 1/(cos(x)) vary quickly between -1
and 1.
We continue our exploration by fixing b = c = 1, k = 5, and
varying a through the animation below.
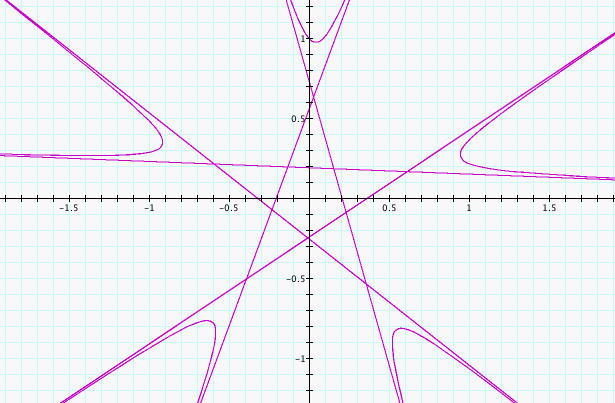
We can see that a affects the size
of the star and how the star is twisted. As the value of a moves
away from 0, the star gets smaller. So the star is biggest when a
= 0. We also notice that as the value of a increases, the star
turns clockwise.
We continue with our exploration by holding a = c = 1, k = 5, and
varying b.
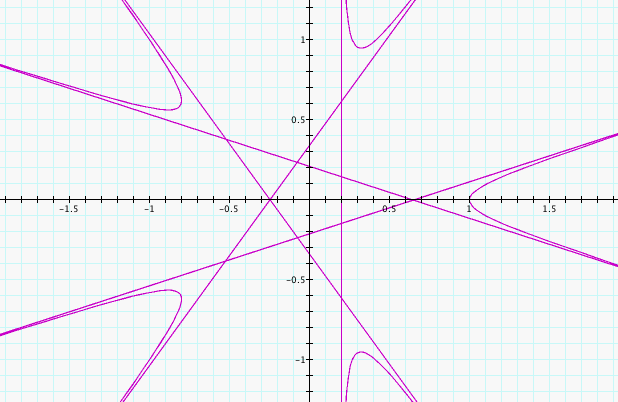
We can see in this animation, that
like a, varying b affects the size and the orientation of the
star. As b moves away from 0, the star gets smaller and
smaller. We also notice that when b = 0 the graph is oriented
with a point on the positive x-axis, but as b moves bigger positively
or negatively, the graph moves so a point is centered either on the
positive y-axis or the negative y-axis respectively. We note
again that the graph moves in a clockwise direction as the value of b
increases.
We conclude our exploration by fixing a = b = 1, k = 5 and varying c.
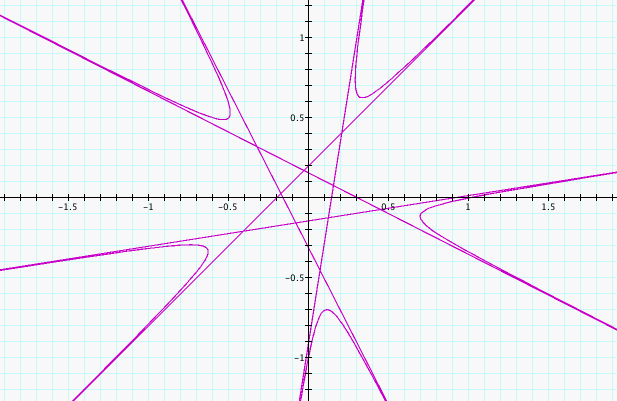
We can immediately see that varying c
has different effects than a and b. For instance, the difference
between c and -c is a precise rotation about the origin of 180
degrees. We also notice that when c = 0, the graph is
empty. Which makes sense, since 0/n = 0 for any n. We also
notice that the value of c mainly affects the size of the star.
As c moves away from 0, the star gets bigger and bigger, regardless of
whether c is moving positively away from 0 or negatively away from 0.
This concludes our exploration.







