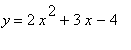 and manipulate it in different ways. The graph of this function can be seen below
and manipulate it in different ways. The graph of this function can be seen below
Sarah Hofmann
EMAT 6680 Summer 2006
Assignment 2
Exercize 6.
Our goal is to look at the graph
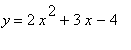 and manipulate it in different ways. The graph of this function can be seen below
and manipulate it in different ways. The graph of this function can be seen below
![[Maple Plot]](images2/assign22.gif)
i) Overlay a new graph replacing each x by (x-4).
![[Maple Plot]](images2/assign23.gif)
We can see that when x is replaced by (x-4) the x-coordinate of the vertex of the parabola moves from -0.75 to 3.25. In other words it shifts to the left by 4 units.
ii) Change the equation to move the graph into the second quadrant.
This is an impossible task. The domain of any parabola is (
![]() ). So there will always be points (x,y) for all negative real numbers x. So the graph of a parabola must appear in either the third and/or the fourth quadrant. Thus it is impossible to isolate a parabola in
one
quadrant. It is however possible to move the parabola entirely above or below the x-axis by vertically shifting and flipping the parabola. For example if we shift the parabola right by four units by replacing x with (x-4), flip the parabola about the x-axis by replacing y with -y, and move it down 6 units by subtracting 6 from the y or adding 9 to the right side of the equation (that is by the equation
). So there will always be points (x,y) for all negative real numbers x. So the graph of a parabola must appear in either the third and/or the fourth quadrant. Thus it is impossible to isolate a parabola in
one
quadrant. It is however possible to move the parabola entirely above or below the x-axis by vertically shifting and flipping the parabola. For example if we shift the parabola right by four units by replacing x with (x-4), flip the parabola about the x-axis by replacing y with -y, and move it down 6 units by subtracting 6 from the y or adding 9 to the right side of the equation (that is by the equation
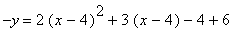 which is equivalent to
which is equivalent to
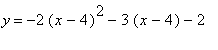 we will get a parabola entirely below the x-axis with the vertex in quadrant 2. Below we have graphed the equations of
we will get a parabola entirely below the x-axis with the vertex in quadrant 2. Below we have graphed the equations of
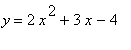 and
and
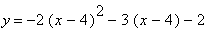 .
.
![[Maple Plot]](images2/assign29.gif)
However, one must hote that if we look at more quadrant space, the second (green) graph will eventually cross over into quadrant 3, as shown below.
![[Maple Plot]](images2/assign210.gif)
iii) Change the equation to produce a graph concave down that shares the same vertex.
It would be easier if we first move the graph so it was concave down. We can do this by rotating it about the x-axis, or by replacing y with -y. So we must graph the equation
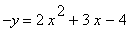 which is equivalent to the equation
which is equivalent to the equation
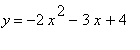 .
.
![[Maple Plot]](images2/assign213.gif)
Now all we need to do is move the graph down. But where should the new vertex be? It should be on the old vertex. Well what is the old vertex? We know the vertex of a parabola is at the point (
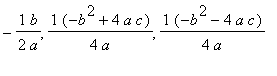 ), so the vertex of the first (red) parabola is at (
), so the vertex of the first (red) parabola is at (
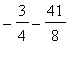 ) and the vertex of the second (green) parabola is at (
) and the vertex of the second (green) parabola is at (
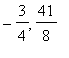 ). So their x-coordinates match. We just need to move the second (green) parabola down so that the y-coordinate is
). So their x-coordinates match. We just need to move the second (green) parabola down so that the y-coordinate is
![]() instead of
instead of
![]() . That is we need to shift the green parabola down
. That is we need to shift the green parabola down
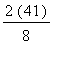 =
=
![]() . So we need to subtract
. So we need to subtract
![]() from our current second (green) equation. So we now want our second (green) equation to be
from our current second (green) equation. So we now want our second (green) equation to be
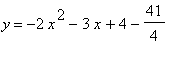 which is equivalent to
which is equivalent to
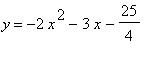 . The graphs of
. The graphs of
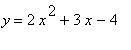 and
and
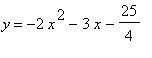 are shown below.
are shown below.
![[Maple Plot]](images2/assign226.gif)
If we check using the above formula we do indeed see that both parabolas have verticies at (
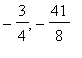 ), as needed.
), as needed.