| Sarah Hofmann EMAT 6680 Summer 2006 Assignment 3 |
| Investigation
1 Our assignment for investigation 1 was to notice that all equations of the form 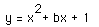 have their
verticies on the equation have their
verticies on the equation 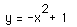 as shown
in the graph below. as shown
in the graph below.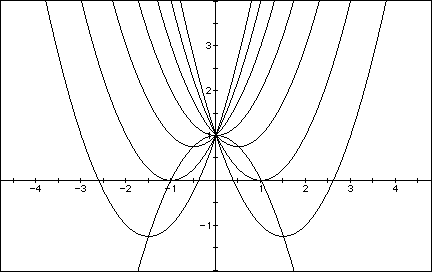 We now need to generalize this idea. |
| Investigation
2 We were to graph the equation 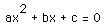 where a = 1 in the xb plane for different values of c. We have chosen to plot the
integers c = -4 . . . 3. where a = 1 in the xb plane for different values of c. We have chosen to plot the
integers c = -4 . . . 3.
 Notice that in the case
where c = 0, the turquoise
line, is linear.
|
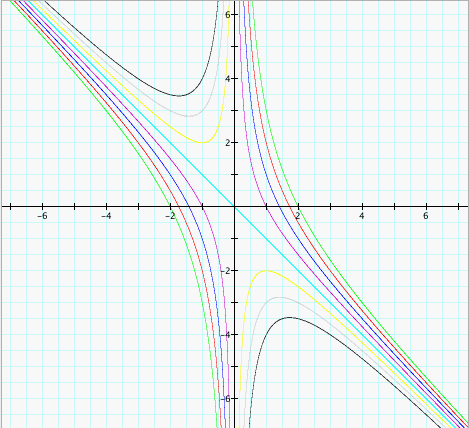
| Investigation
3 Our job for this investigation is to add the equation 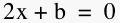 to the above graph and investigate
its relationship to the quadratic formula. We will add the
equation to the above graph in the form to the above graph and investigate
its relationship to the quadratic formula. We will add the
equation to the above graph in the form 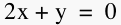 . It will
appear as a purple line. . It will
appear as a purple line.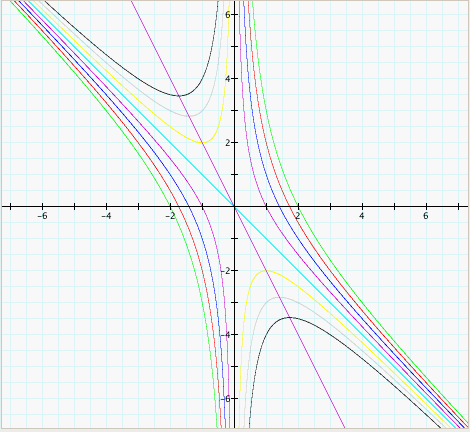 The quadratic formula for our equation with a = 1 is 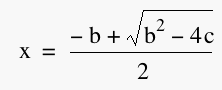 . If we look at the quadratic
equation in the context of the line . If we look at the quadratic
equation in the context of the line 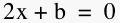 , we can see the following , we can see the following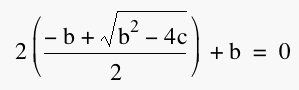 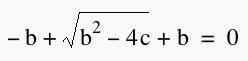  But we know that
 implies that
the
equation has only one root. implies that
the
equation has only one root. |
| Investigation 4. We are to consider graphs in the xc plane for this investigation. If we graph several basic parabolas in the form  for integer values
of c=-4...3, we can see the following graph. for integer values
of c=-4...3, we can see the following graph. 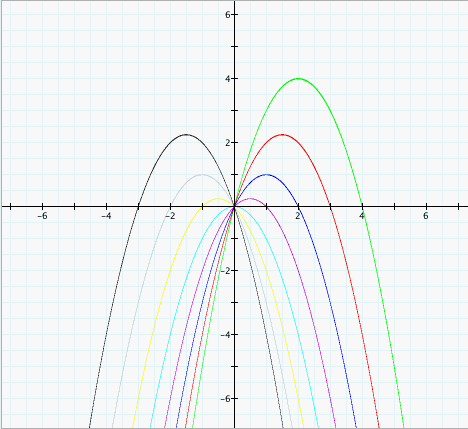 If we differentiate the basic equation, solve for y', and set y' = 0, we can see the first derivative is zero when 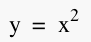 . So the
local maxima occur on this parabola. Indeed if we add the
equation . So the
local maxima occur on this parabola. Indeed if we add the
equation 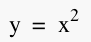 to the above graph we see it
intersects all the parabolas at their verticies. The new parabola
is in purple. to the above graph we see it
intersects all the parabolas at their verticies. The new parabola
is in purple. Now if we consider graphs of the form 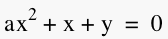 for values of a = -4...3 we can
see the following graphs. for values of a = -4...3 we can
see the following graphs.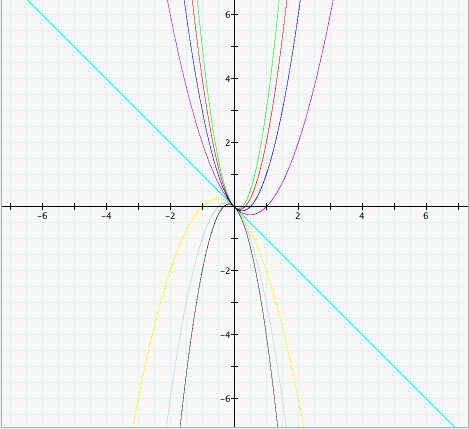 Differentiating the equation 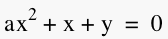 , solving for y',
and setting y'=0 we see that the critical points all coincide on the
line , solving for y',
and setting y'=0 we see that the critical points all coincide on the
line 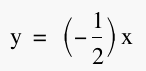 . Indeed if we add this line
as a purple line and zoom in to the above graph we can see it does
cross all the local maxima or minima of the above parabolas. . Indeed if we add this line
as a purple line and zoom in to the above graph we can see it does
cross all the local maxima or minima of the above parabolas.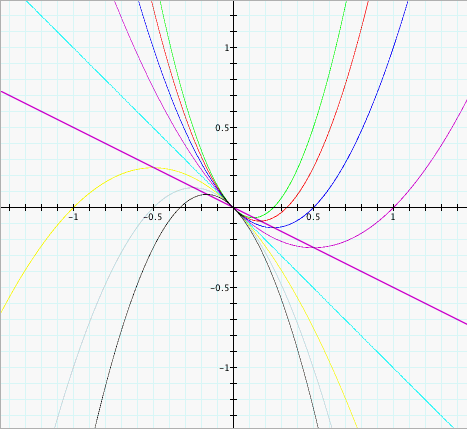 |
| Investigation 5. We are to consider graphs in the xa plane. If we graph several graphs of the basic equation 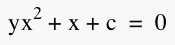 for values of
c=-4...3 we get the following graphs. for values of
c=-4...3 we get the following graphs.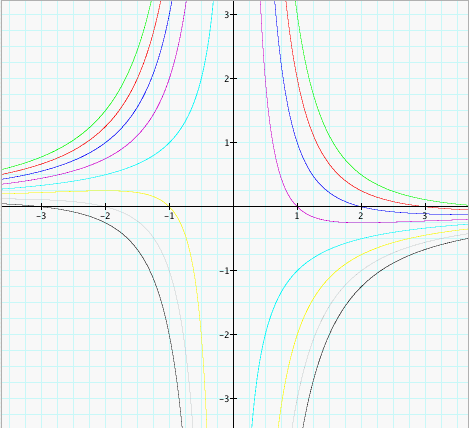 If we consider the basic equation 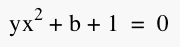 for
integer values of b=-4...3, we get the following graphs. for
integer values of b=-4...3, we get the following graphs. Differentiating the basic equation 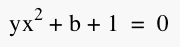 ,
solving for y', setting y'=0, and solving, we see that all the critical
points lie on the equation ,
solving for y', setting y'=0, and solving, we see that all the critical
points lie on the equation 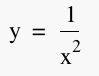 . Adding this equation as a
purple graph to the above graph we see that indeed, all the critical
points pass through the new purple line. . Adding this equation as a
purple graph to the above graph we see that indeed, all the critical
points pass through the new purple line.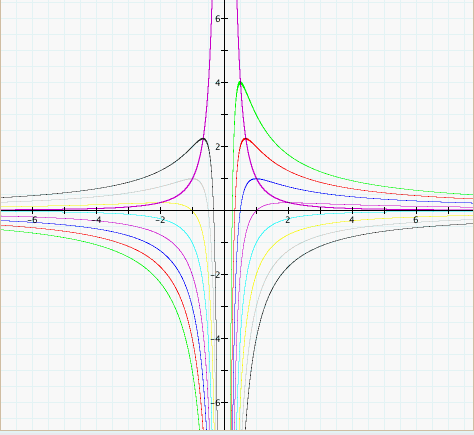 |