Sarah Hofmann
EMAT 6680 Summer 2006
Assignment 4

For this assignment we are to do all the activities in assignment 4 and write up one of the activities.  We have decided to write up activity 12.

Activity 4

We are to prove the following claim:  The perpendicular bisectors of the three segments of a triangle are concurrent.

To complete this proof we will need the following

Lemma:  The locus of points in a plane equidistant from 2 points is the line which is the perpendicular bisector of the line segment joining the 2 points.

Proof of claim: 

     Let ABC be a triangle.
 
Let points D, F, and H be the midpoints of segments AB, BC, and CA respectively.

Let DE, FG, and HK be the perpendicular bisector lines of AB, BC, and CA respectively.



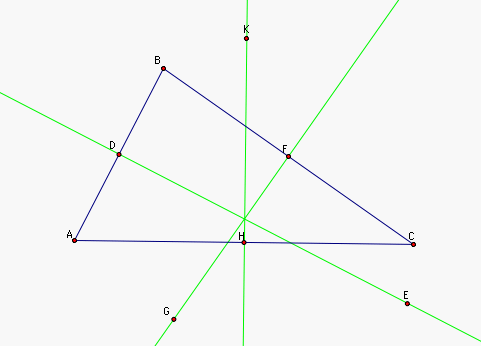
Suppose  HK and DE do not meet at some point O.  Then HK and DE are parallel.  Hence, CA and AB must be parallel or the same segment.  But ABC is a triangle, so this is a contradiction.  Therefore HK and DE meet at some point, call it O.



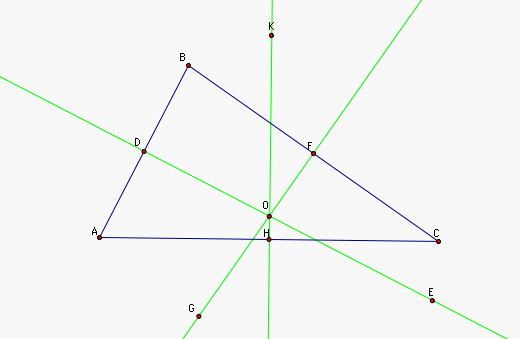
Since O lies on the perpendicular bisectors of AB and CA, by the lemma we know that m(OA) = m(OB) and m(OA) = m(OC).  Then by transitivity, m(OC) = m(OB).



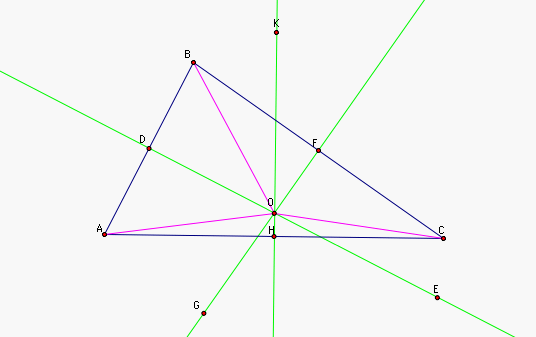
Since m(OB) = m(OC), O lies on the perpendicular bisector of segment BC, by lemma 1.  That is O lies on the line FG.  Thus O lies on DE, FG, and HK.  Therefore the lines CD, FG, and HK are concurent.  That is the perpendicular bisectors of the the three sides of the triangle ABC are concurrent, as needed.