EMAT 6680
Summer 2006
Assignment 6 Problem 3

| Sarah
Hofmann EMAT 6680 Summer 2006 Assignment 6 Problem 3 |
| We have chosen to do
problem number 3 from assignment 6 because it is interesting and
because we have seen a few incorrect solutions in other people's
assignments. We will also attempt a formal proof of why our
solution is in fact correct. |
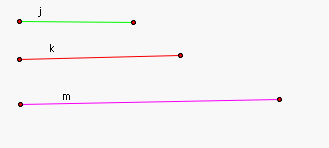
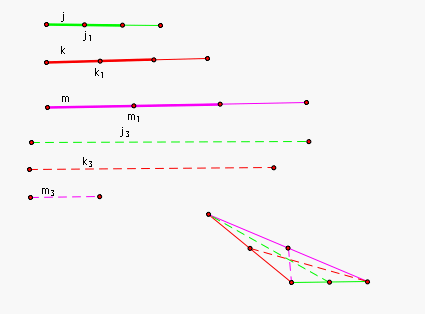
Problem 3 Construct a triangle given the three
medians j,k, and m below. |
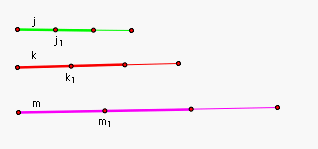
Step 1: Divide each median
into thirds and find segments that are 2/3 the size of each
median. Call the new segments j1, k1, and m1 respectively. |
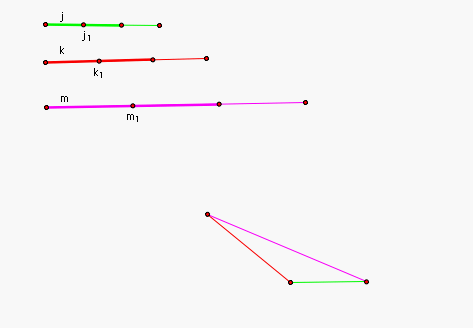
Step 2: Create a triangle
using the 2/3 segments. |
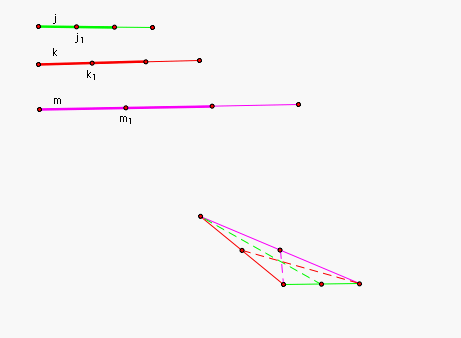
Step 3: Find the medians of
the constructed triangle. |
Step 4: Double the medians
of the new triangle to create the sides of the final triangle.
Call them j3, k3, and m3. |
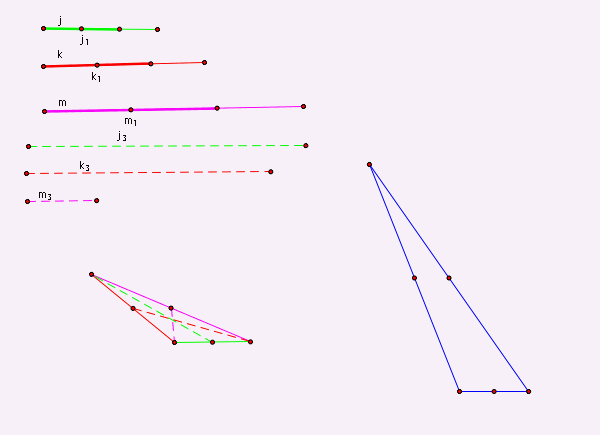
Step 5: Create the new triangle
using j3, k3, and m3. |
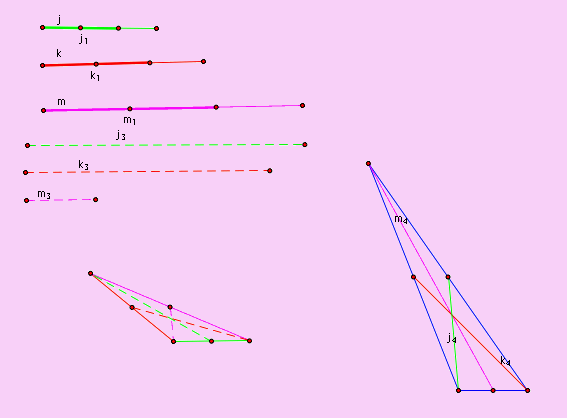
Step 6: Construct medians of
triangle, call them j4, k4, and m4. |
Step 7: Check by measuring and
using circles. |
| As you can see both the
circles
and measurements verify that we have the correct triangle.
However, constructing circles and measuring is NOT PROOF that we have
constructed the proper triangle. So we must now prove that indeed
this is the desired triangle with the correct medians. |
| To do this problem we used
the following fact that we must prove below: Given triangle 1.
Create triangle 2 from the 2/3 the lengths of the medians of triangle
1. Then the medians of triangle 2 will be half the length of the
segments of triangle 1. |
| Proof: |
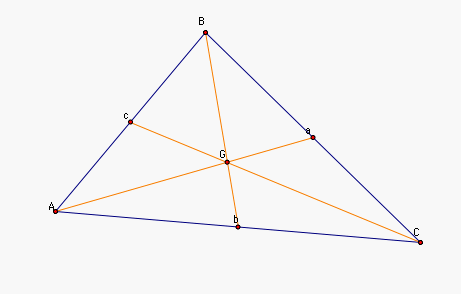
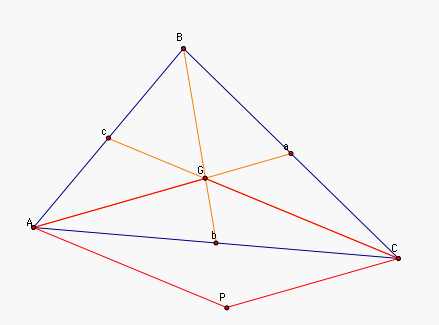
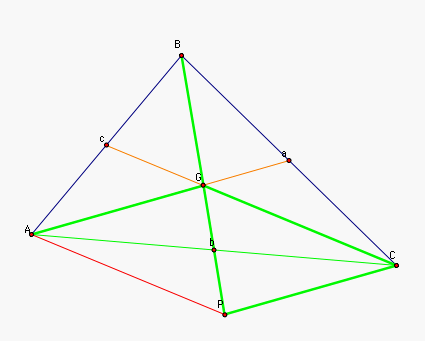
Given a triangle ABC,
construct the midpoints of the sides called a,b, and c, and the
medians, Aa, Bb, and Cc, and label the circumcenter G. |
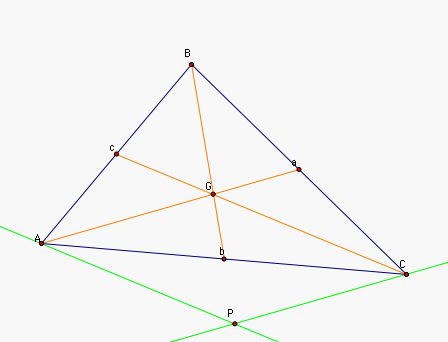
Construct the line through C
parallel to Aa and the line through A parallel to Cc. since Aa
and Cc intersect, these lines intersect. Call their intersection
P.  |
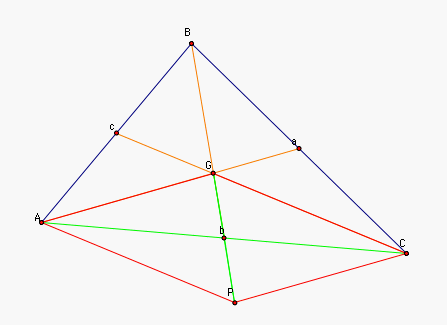
| Now AGCP is a parallelogram by
construction. |
One of the medians of
parallelogram AGCP is AC and the other is GP. Since AGCP is a
parallelogram, the medians AC and GP bisect each other. However,
b is the midpoint of AC. Hence, b is the midpoint of GP. So
m(Gb) = m(bP). |
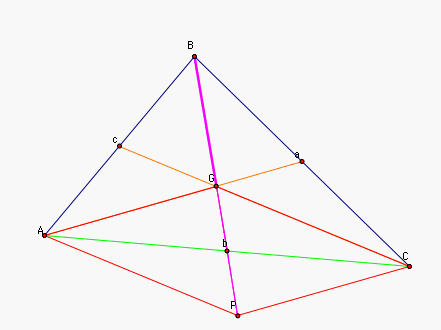
But G divides all the medians of
ABC into 1/3 and 2/3 parts. So m(Gb) = 1/2 m(BG). Thus
m(GP) = m(Gb)+m(bP) = m(Gb)+m(Gb) = 1/2 m(BG) + 1/2 m(BG) =
m(BG). That is m(BP) = m(BG). |
Since m(BP) = m(BG) = 2/3 m(Bb),
m(PC) = m(AG) = 2/3 m(Aa), and m(CG) = 2/3 m(Cc), we have that triangle GPC is a triangle
whose sides are 2/3 the sides of the medians Aa, Bb, and Cc.
We must now show that the medians of triangle GPC are half the lengths
of the sides of ABC.  |
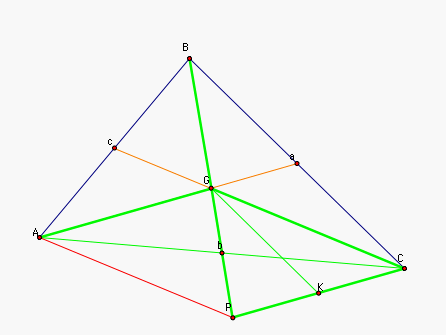
Notice that since b is the
midoint of GP, Cb is a median of triangle GCP. Obviously we
already have that median Cb of GCP is 1/2 the length of AC. That is m(Cb) = 1/2 m(AC), as
needed. Now construct the midpoint K of CP and the median GK. |
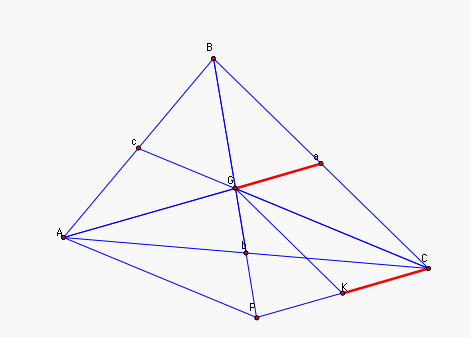
We know PC is parallel to Aa, so
KC is parallel to Ga. We also know m(GA) = m(PC), 1/2 m(GA) =
m(Ga), and 1/2 m(PC) = m(KC). Hence
m(Ga) = 1/2 m(GA) = 1/2 m(PC) = m(KC). So m(Ga) = m(KC).
Hence Ga is equal in length and parallel to KC. |
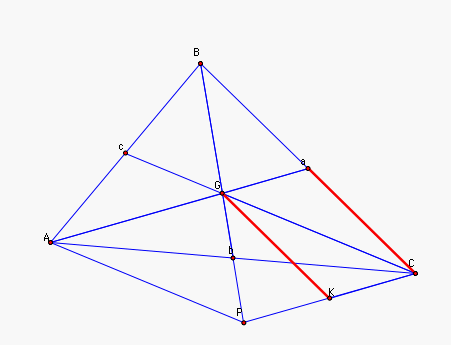
This implies that GaKC is a
parallelogram. So GK is parallel to and equal in length to
Ca. Which implies that GK is parallel to BC and m(GK) = m(Ca) =
1/2 m(BC). That is the median of GK of triangle GPC has length
1/2 a side of triangle ABC (m(GK) =
1/2 m(BC)), as needed. Similarly, we can find that the
third median is 1/2 the length of AB. Thus is is proven. |